7 câu Trắc nghiệm Phép cộng, phép trừ đa thức một biến có đáp án (Thông dụng)
32 người thi tuần này 4.6 2 K lượt thi 7 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 3
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 15: Các trường hợp bằng nhau của tam giác vuông có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. M(x) = 5x4 + x3 + x2 + 2x – 1, hệ số tự do là – 5;
B. M(x) = x4 + x3 + 3x2 + 3, hệ số tự do là 3;
C. M(x) = x4 + x3 + 3x2 + 3, hệ số tự do là 1;
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
M(x) = Q(x) + P(x)
= (3x4 + x3 + 2x2 + x + 1) + (2x4 – x2 + x – 2)
= 3x4 + x3 + 2x2 + x + 1 + 2x4 – x2 + x – 2
= (3x4 + 2x4) + x3 + (2x2 – x2) + (x + x) + (1 – 2)
= 5x4 + x3 + x2 + 2x – 1
Số hạng không chứa biến là – 1, nên hệ số tự do là – 1.
Vậy M(x) = 5x4 + x3 + x2 + 2x – 1, hệ số tự do là – 1.
Câu 2
A. Bậc 3, hệ số cao nhất là 11;
B. Bậc 4 hệ số cao nhất là 11;
C. Bậc 3, hệ số cao nhất là 2;
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
F(x) = A(x) – B(x)
= (5x4 – x3 + 2x2 + 4) – (5x4 – 3x3 + x – 7)
= 5x4 – x3 + 2x2 + 4 – 5x4 + 3x3 – x + 7
= (5x4 – 5x4) + (– x3 + 3x3) + 2x2 – x + (4 + 7)
= 2x3 + 2x2 – x + 11
Vậy F(x) = 2x3 + 2x2 – x + 11 có bậc 3, hệ số cao nhất là 2.
Câu 3
A. N(x) = – x4 – 2x3 – x2 – 3x + 4;
B. N(x) = x4 – 2x3 – x2 – 3x;
C. N(x) = – x4 + 2x3 + 3x2 – 3x + 4;
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
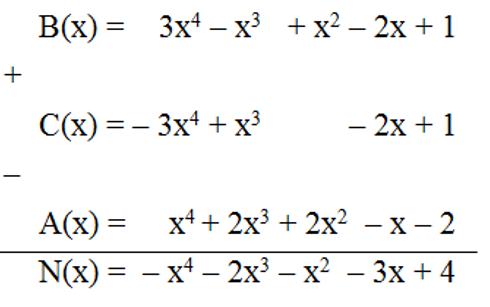
Câu 4
A. 5x4 + x3 + x2 + 2x – 1;
B. x4 + x3 + 3x2 + 3;
C. – x4 – x3 – 3x2 – 3;
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
H(x) + P(x) = Q(x)
nên H(x) = Q(x) – P(x)
= (3x4 + x3 + 2x2 + x + 1) – (2x4 – x2 + x – 2)
= 3x4 + x3 + 2x2 + x + 1 – 2x4 + x2 – x + 2
= (3x4 – 2x4) + x3 + (2x2 + x2) + (x – x) + (1 + 2)
= x4 + x3 + 3x2 + 3
Vậy H(x) = x4 + x3 + 3x2 + 3.
Câu 5
A. P(x) = – x4 + 3x3 – 4x2 + 4x – 5;
B. P(x) = x4 + 3x3 – 4x2 + 4x + 5;
C. P(x) = 5x4 + 3x3 – 4x2 + 4x + 5;
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
3x4 + 5x3 – 5x2 + 5x + 1 – P(x) = 2x4 + 2x3 – x2 + x – 4
P(x) = (3x4 + 5x3 – 5x2 + 5x + 1) – (2x4 + 2x3 – x2 + x – 4)
P(x) = 3x4 + 5x3 – 5x2 + 5x + 1 – 2x4 – 2x3 + x2 – x + 4
P(x) = (3x4 – 2x4) + (5x3 – 2x3) + (– 5x2 + x2) + (5x – x) + (1 + 4)
P(x) = x4 + 3x3 – 4x2 + 4x + 5
Câu 6
Cho Q(x) – (x5 + 2x3 – 2 + x) = 3x3 + 2x2 – 1. Tìm Q(x) rồi sắp xếp theo lũy thừa giảm dần của biến.
Cho Q(x) – (x5 + 2x3 – 2 + x) = 3x3 + 2x2 – 1. Tìm Q(x) rồi sắp xếp theo lũy thừa giảm dần của biến.
A. Q(x) = x5 + 5x3 + 2x2 + x – 3;
B. Q(x) = 5x3 + 2x2 – 3 + x5 + x;
C. Q(x) = – x5 + 5x3 + 2x2 + x + 3;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. P(x) = x5 + x3 + 5x2 + 2x – 1 và Q(x) = x4 + 8x2 + x + 1;
B. P(x) = x4 + x3 + 5x2 + 2x – 1 và Q(x) = x4 + 8x2 – x + 1;
C. P(x) = x4 + x3 + 5x2 + 2x + 1 và Q(x) = x4 + 2x3 + 8x2 – x + 1;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.