Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.
Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.
Quảng cáo
Trả lời:
Giải bởi Vietjack
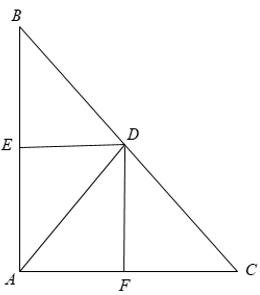
+ Xét tứ giác AEDF có = 900
⇒ AEDF là hình chữ nhật . ( 1 )
Theo giả thiết ta có AD là đường phân giác của góc
⇒ = 450.
+ Xét Δ AED có = 900; = 450 ⇒ = 450
⇒ Δ AED vuông cân tại E nên AE = ED ( 2 )
Từ ( 1 ),( 2 ) ⇒ AEDF là hình vuông (dấu hiệu 1 – mục 3)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
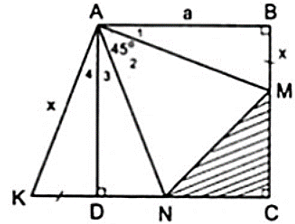
a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
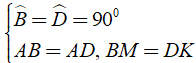
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
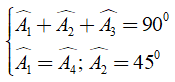
⇒ = 900 - 450 = 450
Lời giải
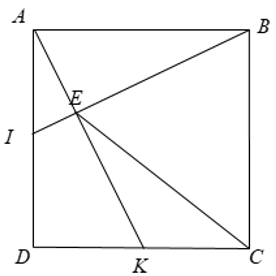
Xét Δ BAI và Δ ADK có:
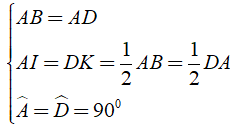
⇒ Δ BAI = Δ ADK ( c - g - c )
⇒ ABIˆ = DAKˆ (góc tương ứng bằng nhau)
Mà = 900 ⇒ = 900
+ Xét Δ ABE có = 1800
⇒ = 1800 - ( ) = 1800 - 900 = 900 hay AK ⊥ BI (đpcm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo