Một vật đồng chất được thả vào một cốc chất lỏng. Ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng. Tìm mối liên hệ giữa trọng lực \(\overrightarrow P \) của vật và lực đẩy Archimedes \(\overrightarrow F \) mà chất lỏng tác động lên vật. Tính tỉ số giữa trọng lượng riêng của vật và của chất lỏng.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 10 Bài 9. Tích của một vectơ với một số có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

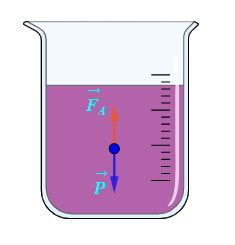
Trọng

lực \(\overrightarrow P \) của vật và lực đẩy Archimedes \(\overrightarrow F \) mà chất lỏng tác động lên vật được mô tả như hình vẽ trên.

Do vật ở trạng thái cân bằng nên hai lực \(\overrightarrow P \)và \(\overrightarrow F \) ngược hướng nhau và có cường độ bằng nhau.

\( \Rightarrow \left| {\overrightarrow P } \right| = \left| {\overrightarrow F } \right|\)

Gọi d và d' là trọng lượng riêng của vật và chất lỏng;

V là thể tích của vật

Khi thả vật vào cốc chất lỏng thì ở trạng thái cân bằng, vật chìm một nửa thể tích trong chất lỏng nên thể tích chất lỏng bị chiếm chỗ là \(\frac{V}{2}.\)

Khi đó trọng lượng của vật là: P = d.V

Và lực đẩy Archimedes mà chất lỏng tác động lên vật là: \({F_A} = d'.\frac{V}{2}.\)

Do đó \[\left| {\overrightarrow P } \right| = \left| {\overrightarrow F } \right| \Leftrightarrow d.V = d'.\frac{V}{2} \Leftrightarrow d = \frac{{d'}}{2} \Leftrightarrow \frac{d}{{d'}} = \frac{1}{2}.\]

Vậy tỉ số giữa trọng lượng riêng của vật và của chất lỏng bằng \(\frac{1}{2}.\)

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O.

Chứng minh rằng ba điểm G, H, O cùng thuộc một đường thẳng.

Xem đáp án

Lời giải

Vì G là trọng tâm tam giác ABC nên \[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} .\]

Mà \[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} \] (câu b)

Suy ra \(\overrightarrow {OH} = 3\overrightarrow {OG} \)

Khi đó \(\overrightarrow {OH} \) và \(\overrightarrow {OG} \) cùng phương, cùng hướng

O, H, G thẳng hàng.

Vậy ba điểm O, H, G thẳng hàng.

Câu 2

Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O.

Chứng minh rằng \[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} .\]

Xem đáp án

Lời giải

Vì

M là trung điểm của BC nên \(\overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {OM} \)

Mà \[\overrightarrow {AH} = 2\overrightarrow {OM} \] (câu a)

\[ \Rightarrow \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {AH} \]

\[ \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {AH} \]

\[ \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} .\]

Vậy \[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} .\]

Câu 3