10 Bài tập Xác định hình chiếu vuông góc của một điểm, một đường thẳng, một tam giác (có lời giải)
48 người thi tuần này 4.6 1.2 K lượt thi 10 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 10
1.7 K lượt thi
38 câu hỏi
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 8
1.7 K lượt thi
38 câu hỏi
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 7
1.7 K lượt thi
38 câu hỏi
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 6
1.7 K lượt thi
38 câu hỏi
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 5
1.7 K lượt thi
38 câu hỏi
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 4
1.7 K lượt thi
38 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 2
1.7 K lượt thi
39 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 1
1.7 K lượt thi
39 câu hỏi
Danh sách câu hỏi:
Câu 1
A. Nếu MH ⊥ (P) tại H thì M là hình chiếu vuông góc của H lên (P);
B. Nếu MH ⊥ (P) tại H thì H là hình chiếu vuông góc của M lên (P);
C. Nếu MH // (P) thì M là hình chiếu vuông góc của H lên (P);
D. Nếu MH // (P) thì H là hình chiếu vuông góc của M lên (P).
Lời giải
Đáp án đúng là: B
Nếu MH ⊥ (P) tại H thì H là hình chiếu vuông góc của M lên (P).
Câu 2
A. SB;
B. CD;
C. AD;
D. BD.
Lời giải
Đáp án đúng là: C
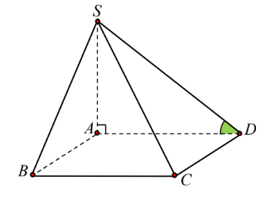
Vì SA vuông góc với mặt đáy nên A là hình chiếu vuông góc của S lên (ABCD).
Vì D thuộc (ABCD) nên D là hình chiếu vuông góc của D lên (ABCD).
Do đó, hình chiếu vuông góc của SD lên (ABCD) là AD.
Câu 3
A. AN;
B. AM;
C. MN;
D. MQ.
Lời giải
Đáp án đúng là: B
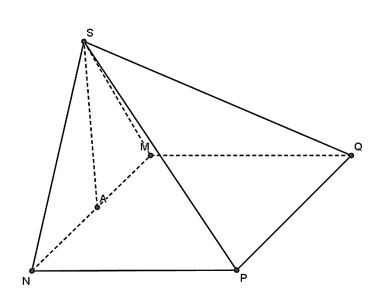
Vì SA vuông góc với đáy nên hình chiếu vuông góc của S lên (MNPQ) là A.
Vì M thuộc (MNPQ) nên hình chiếu vuông góc của M lên (MNPQ) là M.
Do đó, hình chiếu vuông góc của SM lên (MNPQ) là AM.
Câu 4
A. AC với C là trung điểm của PQ;
B. AC với C là trung điểm của MP;
C. AC với C là trung điểm của AQ;
D. AC với C là trung điểm của AP.
Lời giải
Đáp án đúng là: D
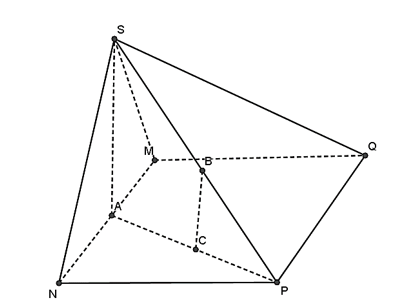
Vì SA vuông góc với đáy nên hình chiếu vuông góc của S lên mặt phẳng (ABCD) là A.
Gọi C là trung điểm của AP ta có:
BC // SA (vì BC là đường trung bình của tam giác SAP)
Mà SA ⊥ (ABCD) nên BC ⊥ (ABCD)
Do đó, C là hình chiếu vuông góc của B lên (ABCD).
Vậy hình chiếu vuông góc của SB lên (ABCD) là AC với C là trung điểm của AP.
Câu 5
A. ∆ACD;
B. ∆BCD;
C. ∆BAD;
D. ∆ABC.
Lời giải
Đáp án đúng là: A
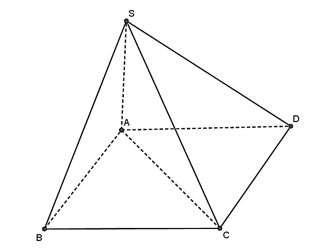
Vì SA vuông góc với đáy nên hình chiếu vuông góc của S lên mặt phẳng (ABCD) là A.
Vì C, D thuộc (ABCD) nên hình chiếu vuông góc của C, D lần lượt là C, D.
Do đó, hình chiếu vuông góc của tam giác SCD lên mặt phẳng (ABCD) là tam giác ACD.
Câu 6
A. Tam giác AB'C' với B', C' lần lượt là trung điểm của AP, BQ;
B. Tam giác AB'C' với B', C' lần lượt là trung điểm của AP, AQ;
C. Tam giác AB'C' với B', C' lần lượt là trung điểm của AP, AN;
D. Tam giác AB'C' với B', C' lần lượt là trung điểm của AM, AQ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. H là trung điểm của AB;
B. H trùng với C;
C. H là trung điểm của BC;
D. H trùng với A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. SB;
B. SM với M là trung điểm của AB;
D. SA;
D. SN với N là trung điểm của SB.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. ID với I là trung điểm SA;
B. BA;
C. ID với I là trọng tâm của tam giác SAD;
D. SD.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. Điểm H với H là trọng tâm của tam giác ABC;
B. Điểm H với H là trung điểm AB;
C. Điểm H với H là trung điểm BC;
D. Điểm H với H là trung điểm AC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập