Gọi (P) là đồ thị hàm số . Trong các đường thẳng sau, đường thẳng nào là tiếp tuyến của (P)?
A. y = -x-3
B. y = 11x+4
C. y = -x+3
D. y = 4x-1
Quảng cáo
Trả lời:
Chọn C.
![]()
Điều kiện để đường thẳng y = ax + b là tiếp tuyến của hàm số y = f(x) (C):
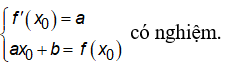
Kiểm tra các đáp án
Đáp án A
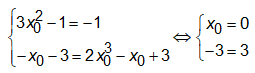
vô lí, đáp án A sai.
Đáp án B:
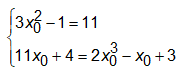

đáp án B sai.
Đáp án C:
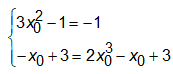
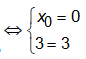
luôn đúng. Đáp án C đúng.
Do đáp án C đúng nên đáp án D sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. f(2) + f(3) = 4
B. f(-1)= 2
C. f(2) = 1
D. f(2018) > f(2019)
Lời giải
Chọn B.
Xét đáp án A:
Ta có:
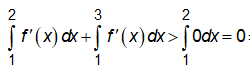
![]()
![]()
nên đáp án A không thể xảy ra.
Xét đáp án C:
Ta có:
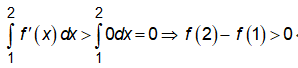
![]()
Nên phương án C không thể xảy ra.
Xét đáp án D:
Ta có:
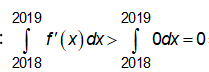
![]()
![]()
nên phương án D không thể xảy ra.
Bằng phương pháp loại suy, ta có đáp án B.
Tuy nhiên, ta có thể chỉ ra một hàm ![]() thỏa mãn đáp án B vì
thỏa mãn đáp án B vì
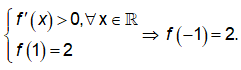
Câu 2
A. (-; 0]
B. [-;+)
C. (-;-]
D. (0;+]
Lời giải
Đáp án C
Phương pháp:
Hàm số y = f(x) nghịch biến trên D khi và chỉ khi ![]() và bằng 0 tại hữu hạn điểm
và bằng 0 tại hữu hạn điểm
Cách giải:
Ta có: ![]()
Hàm số đã cho nghịch biến trên ![]()
![]()
![]()
![]()
![]()
![]()
Xét hàm số: ![]() ta có:
ta có: ![]()
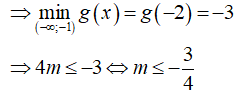
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.