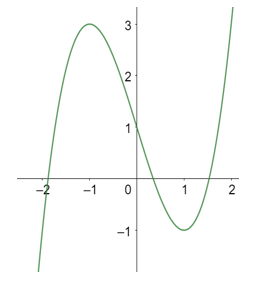
Cho hàm số y = f(x) xác định trên và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + m - 2018 = 0 có duy nhất một nghiệm.
A. m 2015, m 2019.
B. 2015 < m < 2019.
C. m = 2015, m = 2019.
D. m < 2015, m > 2019.
Quảng cáo
Trả lời:
Chọn D
Phương pháp:
Biến đổi phương trình về f(x) = 2018 - m và sử dụng tương giao đồ thị: Phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng y = 2018 - m cắt đồ thị hàm số y = f(x) tại duy nhất một điểm.
Cách giải:
Phương trình f(x) + m - 2018 = 0 ![]()
Đây là phương trình hoành độ giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = 2018 - m (có phương song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có ycbt 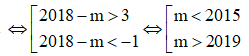
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 1375000.
B. 3781250.
C. 2500000.
D. 3000000.
Lời giải
Chọn A
Phương pháp:
Gọi giá tua là x (triệu đồng).
Lập hàm số tổng doanh thu theo x.
Xét hàm tìm GTLN của hàm số trên và kết luận.
Cách giải:
Gọi x (triệu đồng) là giá tua.
Số tiền được giảm đi so với ban đầu là 2-x.
Số người tham gia được tăng thêm nếu bán với giá x là: ![]()
Số người sẽ tham gia nếu bán giá x là: 150 + (400-200x) = 550 - 220x
Tổng doanh thu là: f(x) = x(550-220x) ![]()
![]()
Bảng biến thiên
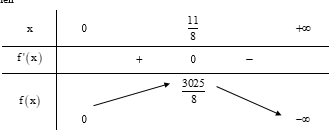
Dựa vào bảng biến thiên ta thấy f(x) đạt giá trị lớn nhất khi ![]()
Vậy công ty cần đặt gói tua 1375000 đồng thì tổng doanh thu sẽ cao nhất là 378125000 đồng.
Câu 2
A. Hàm số y = f(x) +1 đồng biến trên khoảng (a;b)
B. Hàm số y = -f(x) + 1 nghịch biến trên khoảng (a;b).
C. Hàm số y = f(x) +1 đồng biến trên khoảng (a;b).
D. Hàm số y = -f(x) -1 nghịch biến trên khoảng (a;b)
Lời giải
Chọn A
Theo giả thiết ta có ![]() (dấu bằng xảy ra tại hữu hạn điểm thuộc (a; b)).
(dấu bằng xảy ra tại hữu hạn điểm thuộc (a; b)).
Trên khoảng (a; b)
- Hàm số y = f(x) + 1 có đạo hàm bằng f’(x) nên C đúng.
- Các hàm số y = - f(x) + 1 và y = - f(x ) - 1 có đạo hàm bằng - f’(x) nên B, D đúng.
Do đó A sai
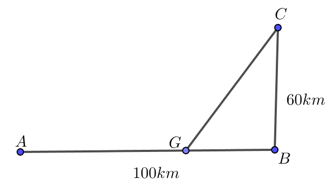
Câu 3
A. 50 (km)
B. 60 (km)
C. 55 (km)
D. 45 (km)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 999.
B. 1001.
C. 1998.
D. 1000.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.