3 câu Trắc nghiệm Đường trung trực của một đoạn thẳng có đáp án (Vận dụng)
21 người thi tuần này 4.6 1.8 K lượt thi 3 câu hỏi 30 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
23.8 K lượt thi
15 câu hỏi
Bài tập: Đồ thị của hàm số y = ax có đáp án
6.2 K lượt thi
23 câu hỏi
19 câu Trắc nghiệm Toán 7 Bài 6: Tam giác cân có đáp án (Vận dụng)
4.7 K lượt thi
19 câu hỏi
9 câu Trắc nghiệm Toán 7 Bài 7: Định lí Pi-ta-go có đáp án (Vận dụng)
4.1 K lượt thi
9 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. AH ⊥ BC;
B. AH là đường trung trực của đoạn thẳng BC;
C. HB = HC;
D. HA = HB.
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
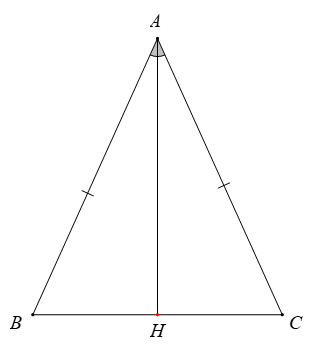
Xét tam giác ABH và tam giác ACH có:
AB = AC (∆ABC cân tại A)
(AH là đường phân giác của )
AH là cạnh chung
Do đó, ∆ABH = ∆ACH (c.g.c)
⇒ HB = HC (hai cạnh tương ứng) (1)
Và (hai góc tương ứng)
Mà (hai góc kề bù)
⇒⇒ AH ⊥ BC (2)
Từ (1) và (2) ⇒AH là đường trung trực của đoạn thẳng BC.
Câu 2
A. ∆AMO = ∆BNO;
B. ∆AMN cân tại A;
C. ∆AMB cân tại A;
D. ∆ANB cân tại N.
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
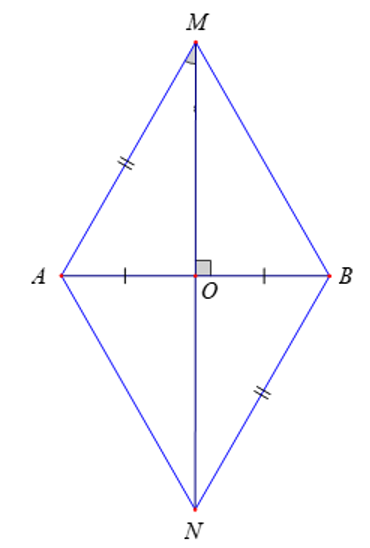
MN là đường trung trực của AB ⇒ MN ⊥ AB tại O và OA = OB
+) Xét hai tam giác vuông AMO và BNO có:
AM = BN (theo giả thiết)
OA = OB
⇒ ∆AMO = ∆BNO (cạnh huyền – cạnh góc vuông)
+) Ta có: AN = BN (vì N thuộc đường trung trực của AB) ⇒ ∆ANB cân tại N.
Mà AM = BN (theo giả thiết)
⇒ AN = AM
⇒ ∆AMN cân tại A (đpcm)
+) Có: MA = MB (vì M thuộc đường trung trực của AB)
⇒ ∆AMB là tam giác cân tại M.
Câu 3
A. Chu vi ∆AFB nhỏ hơn chu vi ∆AMB;
B. Chu vi ∆AFB lớn hơn chu vi ∆AMB;
C. Chu vi ∆AFB bằng chu vi ∆AMB;
D. Không đủ dữ kiện để so sánh.
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
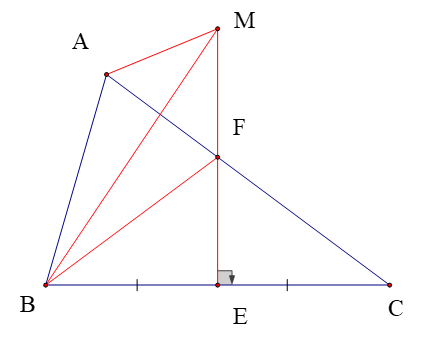
Ta có: FE là đường trung trực của BC (giả thiết)
⇒ FB = FC (tính chất đường trung trực)
M thuộc đường trung trực của BC ⇒ MB = MC (tính chất đường trung trực)
Chu vi ∆AFB = AB + AF + FB = AB + AF + FC = AB + AC
Chu vi ∆AMB = AB + AM + MB = AB + AM + MC
Xét ∆AMC có: AM + MC > AC (bất đẳng thức tam giác)
Do đó: AB + AC < AB + AM + MC
Hay chu vi ∆AFB nhỏ hơn chu vi ∆AMB.
Nhắn tin Zalo