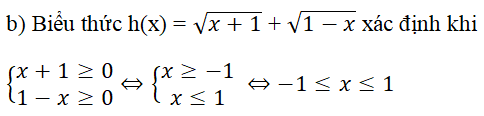Bài 1: Hàm số
30 người thi tuần này 4.6 10.4 K lượt thi 18 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) -Đề 3
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) -Đề 2
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) - Đề 1
Đề kiểm tra Vị trí tương đối giữa hai đường thẳng.góc và khoảng cách (có lời giải) - Đề 3
Đề kiểm tra Vị trí tương đối giữa hai đường thẳng.góc và khoảng cách (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Sự phụ thuộc về quãng đường đi được của 1 xe khách với vận tốc và thời gian.
Lời giải
Các hàm số đã học là; hàm số bậc nhất y = ax + b; hàm số y = ax2
Lời giải
Biểu thức xác định khi x + 2 ≠ 0 ⇔ x ≠ – 2.
Vậy tập xác định của hàm số là D = ℝ\{– 2}.
Lời giải
TXĐ của hàm số là D = [-1;1]
Lời giải
x = -2 ⇒ y = -(-2)2 = -4
x = 5 ⇒ y = 2.5 + 1 = 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.