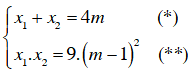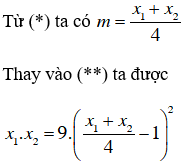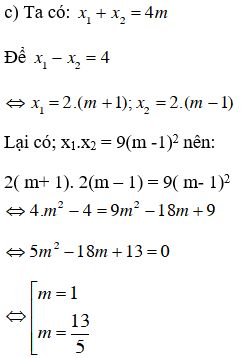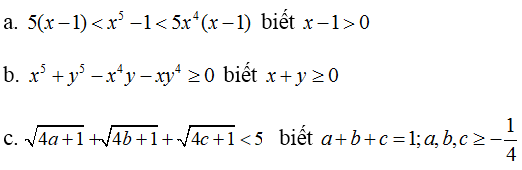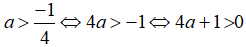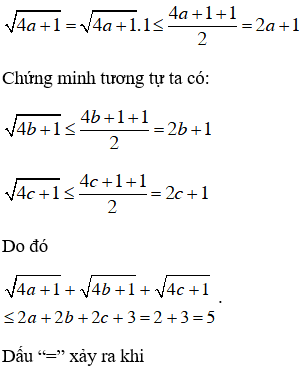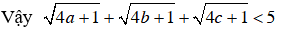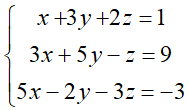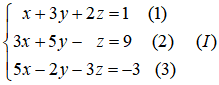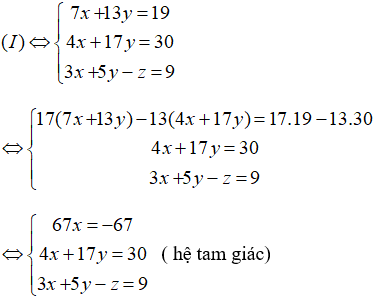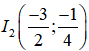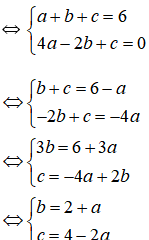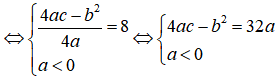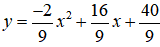Ôn tập cuối năm

a) mx2 – 2x – 4m – 1 = 0 (1)

Với m ≠ 0, ta có:

Δ’ = 1 + m.(4m + 1) = 4m2 + m + 1

=  với mọi m.

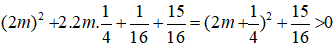
Hay phương trình (1) có hai nghiệm phân biệt với mọi m ≠ 0.

b) x = -1 là nghiệm của phương trình (1)

⇔ m.(-1)2 – 2.(-1) – 4m – 1 = 0

⇔ m + 2 - 4m = 0

⇔ -3m + 1 = 0

⇔ m = 1/3.

Vậy với m = 1/3 thì phương trình (1) nhận -1 là nghiệm.

Khi đó theo định lý Vi-et ta có: x2 + (-1) = 2/m (x2 là nghiệm còn lại của (1))

⇒ x2 = 2/m + 1= 6 + 1 = 7.

Vậy nghiệm còn lại của (1) là 7.

a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)

Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9

Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0

⇔ -5m2 + 18m – 9 ≥ 0

⇔ 5m2 - 18m + 9 ≤ 0

⇔ (5m – 3)(m – 3) ≤ 0

⇔ 3/5 ≤ m ≤ 3.

b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:

+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.

Thử lại:

+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4

+ m = 13/5, (1) trở thành 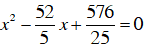 có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.

Vậy m = 1 hoặc m = 13/5.

a) Ta có: x5 – 1 = (x – 1)(x4 + x3 + x2 + x + 1)

Lại có: x – 1 > 0 ⇒ x > 1 ⇒ x5 > x4 > x3 > x2 > x > 1

⇒ 1 + 1 + 1 + 1 + 1 < x4 + x3 + x2 + x + 1 < x4 + x4 + x4 + x4 + x4

hay 5 < x4 + x3 + x2 + x + 1 < 5x4

⇒ 5.(x – 1) < (x – 1)(x4 + x3 + x2 + x + 1) < 5x4.(x – 1)

hay 5.(x – 1) < x5 – 1 < 5x4.(x – 1) (đpcm)

b) x5 + y5 – x4y – xy4 = (x5 - x4y) - (xy4 - y5)

= x4.(x – y) – y4.(x – y)

= (x4 – y4).(x – y)

= (x2 + y2)(x2 – y2)(x – y)

= (x2 + y2).(x + y)(x – y)(x – y)

= (x2 + y2)(x + y)(x – y)2

Mà x2 + y2 ≥ 0; x + y ≥ 0; (x – y)2 ≥ 0

⇒ x5 + y5 – x4y – xy4 ≥ 0.

c) Ta có: 

Tương tự. 4b +1 >0 và 4c +1 > 0

Áp dụng bất đẳng thức Cô-si cho hai số dương 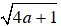 và 1 ta có:

Không có giá trị nào của a, b, c thỏa mãn hệ trên nên dấu “=” của BĐT không xảy ra.

Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và nhân phương trình (2) với 3 rồi trừ đi phương trình (3), phương trình (2) giữ nguyên ta được:

Giải hệ phương trình trên ta được x = -1; y = 2; z = -2.

Vậy hệ phương trình có nghiệm (x; y; z) = (-1; 2; -2)

a) f(x) = 2x.(x+2) - (x+2)(x+1) = 2x2 + 4x - (x2 + 3x + 2) = x2 + x - 2

Tam thức x2 + x – 2 có hai nghiệm x1 = -2 và x2 = 1, hệ số a = 1 > 0.

Vậy:

+ f(x) > 0 nếu x > x2 = 1 hoặc x < x1 = -2, hay x ∈ (-∞; -2) ∪ (1; + ∞)

+ f(x) < 0 nếu x1 < x < x2 hay x ∈ (-2; 1)

+ f(x) = 0 nếu x = -2 hoặc x = 1.

b)

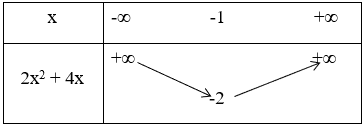
* Hàm số y = 2x(x+2) = 2x2 + 4x có đồ thị (C1) là parabol có:

+ Tập xác định: D = R

+ Đỉnh I1( -1; -2)

+ Trục đối xứng: x = -1

+ Giao điểm với trục tung tại gốc tọa độ.

+ Giao điểm với trục hoành tại O(0; 0) và M(-2; 0).

+ Bảng biến thiên:

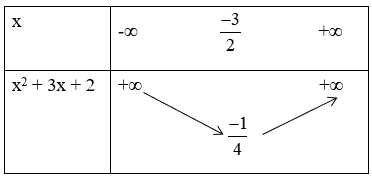
* Hàm số y = (x + 2)(x+1) = x2 + 3x + 2 có đồ thị (C2) là parabol có:

+ Tập xác định D = R.

+ Đỉnh 

+ Trục đối xứng: x = -3/2

+ Giao với trục tung tại D(0; 2)

+ Giao với trục hoành tại M(-2; 0) và E(-1; 0)

+ Bảng biến thiên

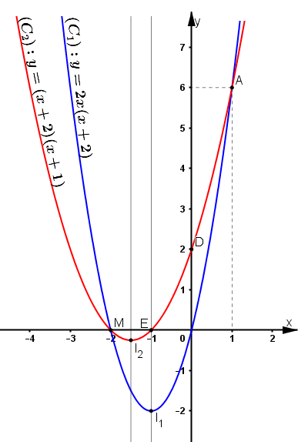
* Đồ thị:

* Tìm tọa độ giao điểm:

Cách 1: Dựa vào đồ thị hàm số:

Nhìn vào đồ thị thấy (C1) cắt (C2) tại A(1; 6) và B ≡ M(-2; 0)

Cách 2: Tính:

Hoành độ giao điểm của (C1) và (C2) là nghiệm của phương trình:

2x(x + 2) = (x + 2)(x + 1)

⇔ (x + 2).2x – (x + 2)(x + 1) = 0

⇔ (x + 2).(2x – x – 1) = 0

⇔ (x + 2).(x – 1) = 0

⇔ x = -2 hoặc x = 1.

+ x = -2 ⇒ y = 0. Ta có giao điểm B(-2; 0)

+ x = 1 ⇒ y = 6. Ta có giao điểm A(1; 6).

c)

+ Đồ thị hàm số y = ax2 + bx + c đi qua điểm A(1; 6) và B(-2; 0)

⇔ tọa độ A và B thỏa mãn phương trình y = ax2 + bx + c

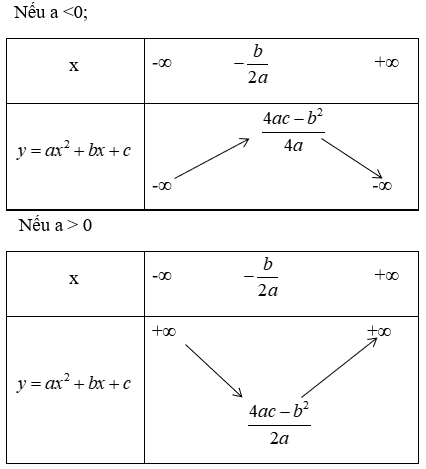
+ Ta có bảng biến thiên của hàm số y = ax2 + bx + c:

Nhận thấy y đạt giá trị lớn nhất bằng 8

Thay b = 2 + a và c = 4 – 2a vào biểu thức 4ac – b2 = 32a ta được:

4.a.(4 – 2a) – (2 + a)2 = 32a

⇔ 16a – 8a2 – (a2 + 4a + 4) = 32a

⇔ 16a– 8a2 – a2 – 4a - 4 – 32a = 0

⇔ -9a2 - 20a - 4 = 0

⇔ a = -2 hoặc a = -2/9.

Nếu a = -2 ⇒ b = 0, c = 8, hàm số y = -2x2 + 8

Nếu a = -2/9 ⇒ b = 16/9, c = 40/9, hàm số