Bài 1: Hàm số lượng giác
31 người thi tuần này 5.0 61.5 K lượt thi 15 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
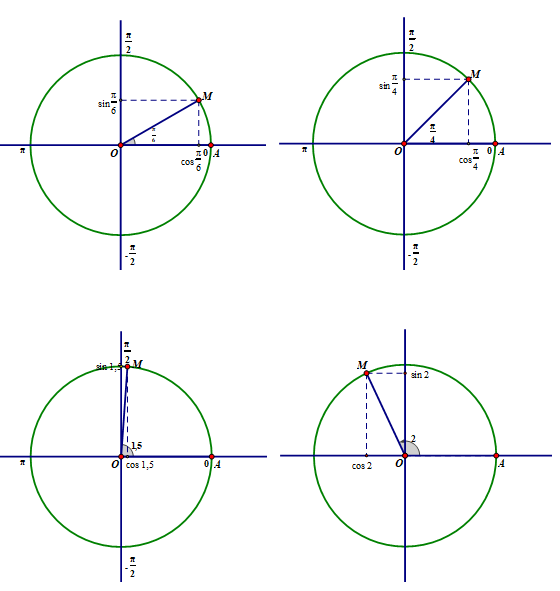
sin π/6 = 1/2; cos π/6 = √3/2
sin π/4 = √2/2; cos π/4 = √2/2
sin 1,5 = 0,9975; cos 1,5 = 0,0707
sin 2 = 0,9093; cos 2 = -0,4161
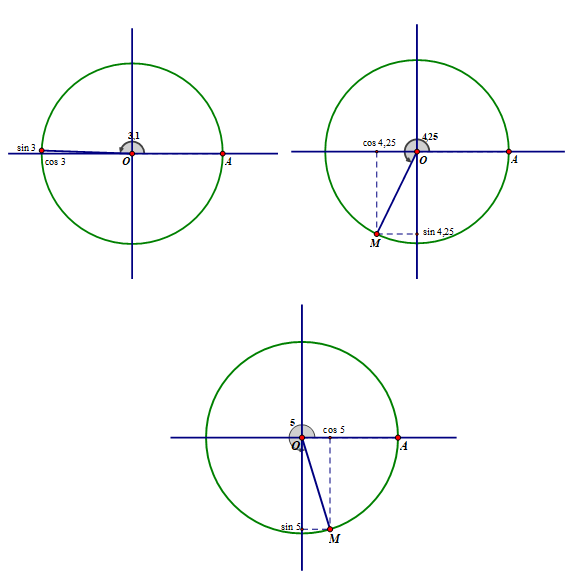
sin 3,1 = 0,0416; cos 3,1 = -0,9991
sin 4,25 = -0,8950; cos 4,25 = -0,4461
sin 5 = -0,9589; cos 5 = 0,2837
Lời giải
sin x = -sin(-x)
cosx = cos(-x)
Lời giải
a) T = k2π (k ∈ Z)
b) T = kπ (k ∈ Z)
Lời giải
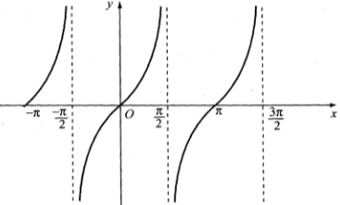
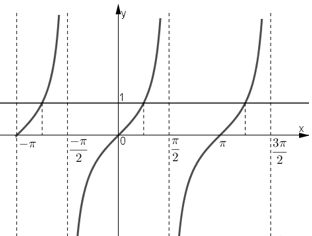
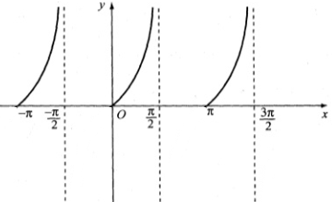
Quan sát đồ thị hàm số y = tan x trên đoạn [-π; 3π/2].
a. tan x = 0 tại các giá trị x = -π; 0; π.
(Các điểm trục hoành cắt đồ thị hàm số y = tanx).
b. tan x = 1 tại các giá trị x = -3π/4; π/4; 5π/4.
c. tan x > 0 với x ∈ (-π; -π/2) ∪ (0; π/2) ∪ (π; 3π/2).
(Quan sát hình dưới)
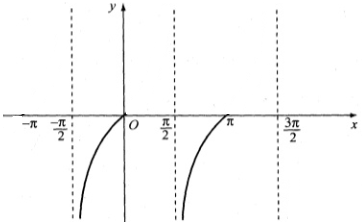
d. tan x < 0 khi x ∈ [-π/2; 0) ∪ [π/2; π)
(Quan sát hình dưới).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.