10 Bài tập Chứng minh các yếu tố hình học liên quan (có lời giải)

Đáp án đúng là: C

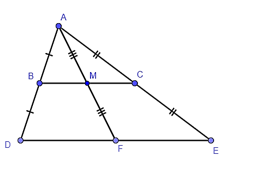
Vì AC = CE nên CE = 6 cm.

Từ giả thiết, ta có tam giác ADE có B là trung điểm của AD, C là trung điểm của AE.

Do đó BC là đường trung bình của tam giác ADE.

Suy ra $\text{BC}=\frac{1}{2}\text{DE}$ , BC // DE (tính chất đường trung bình của tam giác).

Hay DE = 2BC = 2 ⋅ 8 = 16 (cm).

Trong tam giác ADF có B là trung điểm của AD, M là trung điểm của AF.

Do đó BM là đường trung bình của tam giác ADF.

Suy ra BM // DF (tính chất đường trung bình của tam giác).

Hay BC // DF (M ∈ BC).

Vì BC // DE và BC // DF nên D, E, F thẳng hàng.

Vậy đáp án C đúng.

Đáp án đúng là: D

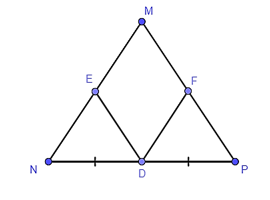
Trong tam giác MNP có:

+ D là trung điểm của NP, DE // MP, E ∈ MN.

Do đó E là trung điểm của MN (tính chất đường trung bình của tam giác).

Suy ra ME = EN = $\frac{1}{2}$MN (1).

+ D là trung điểm của NP, DF // MN, F ∈ MP.

Do đó F là trung điểm của MP (tính chất đường trung bình của tam giác).

Suy ra MF = FP = $\frac{1}{2}$ MP (2).

Mà tam giác MNP cân tại M nên MN = MP (3).

Từ (1), (2), (3) suy ra ME = EN = MF = FP.

Đáp án đúng là: A

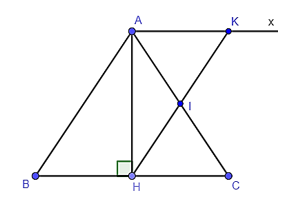
Vì tam giác ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến.

Suy ra H là trung điểm của BC.

Trong tam giác ABC có H là trung điểm của BC, I là trung điểm của AC.

Do đó HI là đường trung bình của tam giác ABC.

Suy ra HI // AB (tính chất đường trung bình của tam giác).

Vì K ∈ HI nên HK // AB.

Đáp án đúng là: C

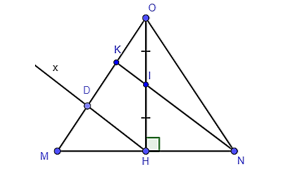
Vì tam giác OMN cân tại O nên OH vừa là đường cao vừa là đường trung tuyến.

Suy ra H là trung điểm của MN.

Trong tam giác MKN có H là trung điểm của MN, DH // KN, D ∈ MK.

Do đó D là trung điểm của MK.

Suy ra MD = DK (1).

Trong tam giác ODH có I là trung điểm của OH, KI // DH (do I ∈ NK), K ∈ OD.

Do đó K là trung điểm của OD.

Suy ra OK = DK (2).

Lại có OK + DK + MD = OM (3).

Từ (1), (2), (3) suy ra OM = 3OK.

Đáp án đúng là: C

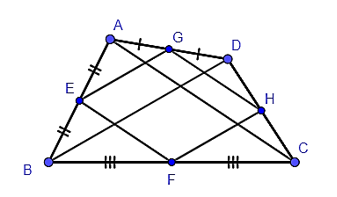
Trong tam giác ABD có E là trung điểm của AB, G là trung điểm của AD

Do đó EG là đường trung bình của tam giác ABD.

Suy ra $\text{EG}=\frac{1}{2}\text{BD}$  (tính chất đường trung bình của tam giác).

Trong tam giác CBD có F là trung điểm của BC, H là trung điểm của CD

Do đó FH là đường trung bình của tam giác CBD.

Suy ra $\text{FH}=\frac{1}{2}\text{BD }$ (tính chất đường trung bình của tam giác).

Trong tam giác ADC có H là trung điểm của DC, G là trung điểm của AD

Do đó HG là đường trung bình của tam giác ADC.

Suy ra $\text{HG}=\frac{1}{2}\text{AC}$  (tính chất đường trung bình của tam giác).

Trong tam giác ABC có E là trung điểm của AB, F là trung điểm của BC

Do đó EF là đường trung bình của tam giác ABC.

Suy ra $\text{EF}=\frac{1}{2}\text{AC}$ (tính chất đường trung bình của tam giác).

Ta có EF + FH + HG + GE = $\frac{1}{2}\text{AC+}\frac{1}{2}\text{BD\hspace{0.17em}+}\frac{1}{2}\text{AC+}\frac{1}{2}\text{BD}$ = AC + BD.