Cho tam giác ABC. Gọi D, E, F theo thứ tự là trung điểm của các cạnh BC, CA. AB.
Xác định điểm M thoả mãn \[\overrightarrow {{\rm{AF}}} - \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {MA} .\]
Quảng cáo
Trả lời:
Lời giải
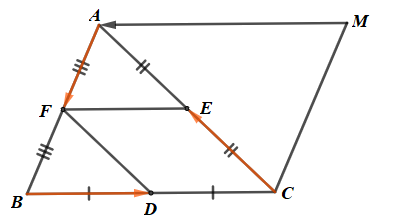
Điểm M thoả mãn \[\overrightarrow {{\rm{AF}}} - \overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {MA} .\]
Mà \[\overrightarrow {AF} --\overrightarrow {BD} + \overrightarrow {CE} = \overrightarrow {CB} \] (câu a)
Nên \(\overrightarrow {MA} = \overrightarrow {CB} \)
Do đó MABC là hình bình hành (theo kết quả bài tập 4.3 SGK Toán 10 tập 1)
Vậy điểm M thoả mãn tứ giác MABC là hình bình hành.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
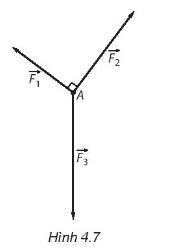
Ta sử dụng các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) và \(\overrightarrow {AE} \) lần lượt biểu diễn cho các lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) và hợp lực \(\overrightarrow F \) của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) (hình vẽ dưới đây).
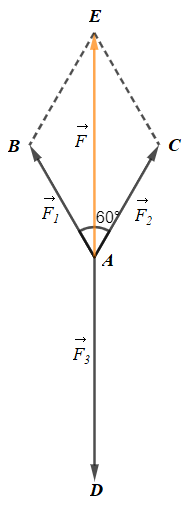
Khi đó do \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) nên tứ giác ABEC là hình bình hành
Lại có góc giữa hai vectơ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) bằng 60° nên \(\widehat {BAC} = 60^\circ \)
Suy ra \(\widehat {ECA} = 180^\circ - \widehat {BAC} = 180^\circ - 60^\circ = 120^\circ \)
Áp dụng định lí Cosin cho tam giác AEC ta có:
AE2 = AC2 + EC2 – 2.AC.EC.cos\(\widehat {ECA}\)
Hay \(A{E^2} = {\left( {2\sqrt 3 } \right)^2} + {\left( {2\sqrt 3 } \right)^2} - 2.2\sqrt 3 .2\sqrt 3 .c{\rm{os120}}^\circ \)
AE2 = 36
AE = 6
Do đó \(\left| {\overrightarrow F } \right| = 6\,\left( N \right)\)
Vì chất điểm A ở trạng thái cân bằng nên hai lực \(\overrightarrow F \) và \(\overrightarrow {{F_3}} \) ngược hướng và có cường độ bằng nhau
Tức là hai vectơ \(\overrightarrow {AE} \) và \(\overrightarrow {AD} \) là hai vectơ đối nhau
Do đó độ lớn của lực \(\overrightarrow {{F_3}} \) bằng \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow F } \right| = 6\,\left( N \right)\)
Vậy độ lớn của lực \(\overrightarrow {{F_3}} \) bằng 6 N.
Lời giải
Lời giải
Ta sử dụng các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) và \(\overrightarrow {AE} \) lần lượt biểu diễn cho các lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) và hợp lực \(\overrightarrow F \) của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) (hình vẽ dưới đây).
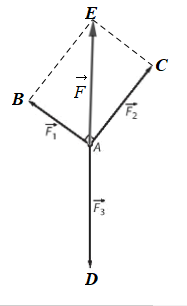
Khi
đó do \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) nên tứ giác ABEC là hình bình hành
Lại có \(\widehat {BAC} = 90^\circ \) nên ABEC là hình chữ nhật
Khi đó \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AE} } \right| = AE = \sqrt {A{B^2} + B{E^2}} \) (định lí Pythagoras)
Hay \(\left| {\overrightarrow F } \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2}} = \sqrt {{{30}^2} + {{40}^2}} = 50\) (N).
Do vật ở vị trí cân bằng A nên hai lực \(\overrightarrow F \) và \(\overrightarrow {{F_3}} \) ngược hướng và có cường độ bằng nhau
Tức là hai vectơ \(\overrightarrow {AE} \) và \(\overrightarrow {AD} \) là hai vectơ đối nhau
Do đó cường độ của lực \(\overrightarrow {{F_3}} \) bằng \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow F } \right| = 50\left( N \right)\)
Vậy cường độ của lực \(\overrightarrow {{F_3}} \) bằng 50 N.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.