3 câu Trắc nghiệm Hai đường thẳng song song có đáp án (Vận dụng)

Hướng dẫn giải

Đáp án đúng là: A

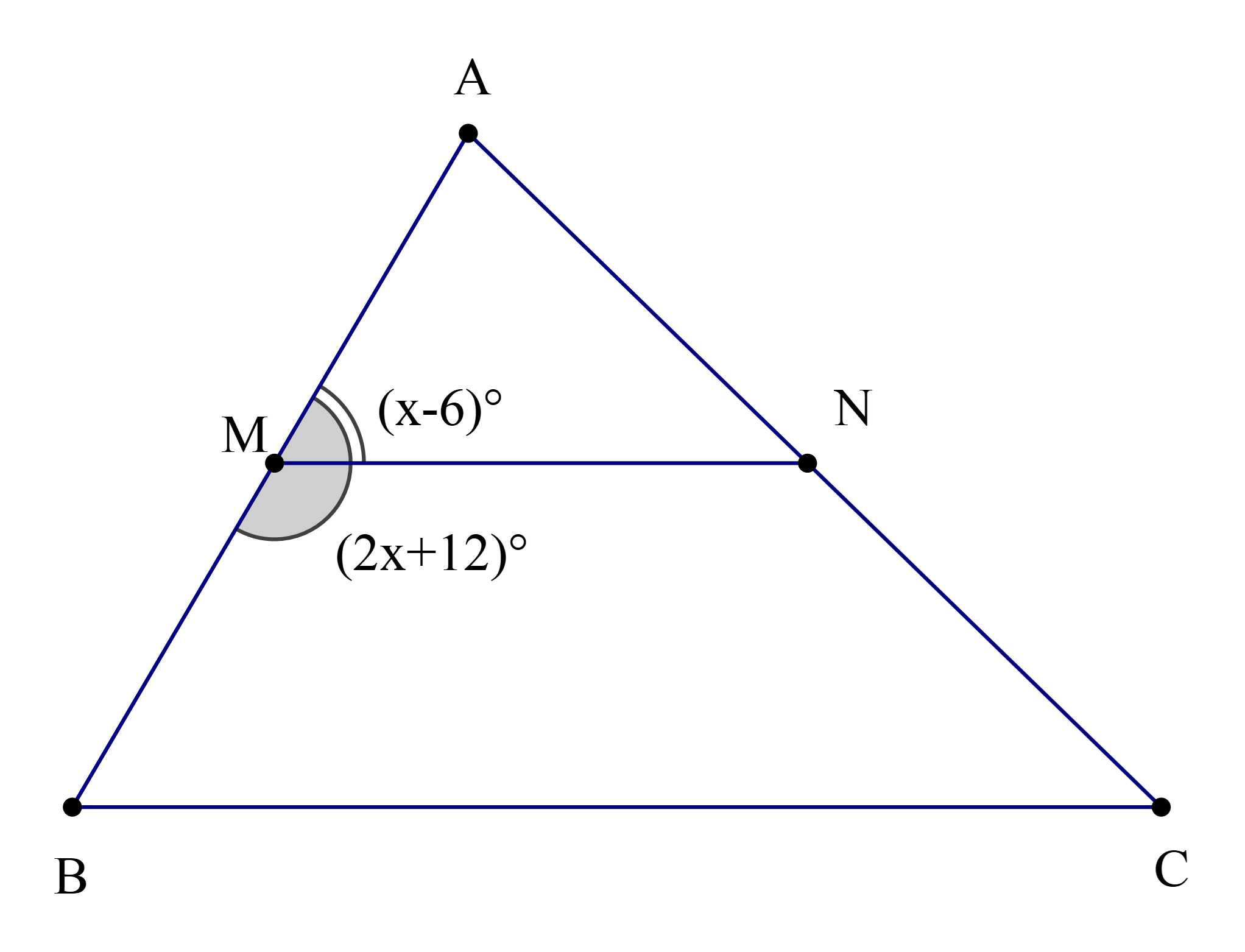
Ta có \(\widehat {{\rm{AMN}}} + \widehat {{\rm{NMB}}} = 180^\circ \) (hai góc kề bù)

Nên (x – 6)° + (2x + 12)° = 180°

Do đó (x – 6 + 2x + 12)° = 180°

Suy ra x – 6 + 2x + 12 = 180

Hay 3x = 180 + 6 – 12 = 174

Suy x = 58

Do đó \(\widehat {{\rm{AMN}}} = (x - 6)^\circ = (58 - 6)^\circ = 52^\circ \)

Vì MN // BC nên \(\widehat {{\rm{AMN}}} = \widehat {{\rm{MBC}}} = 52^\circ \) (hai góc đồng vị)

Hay \(\widehat {{\rm{ABC}}} = 52^\circ \)

Vậy ta chọn phương án A.

Hướng dẫn giải

Đáp án đúng là: D

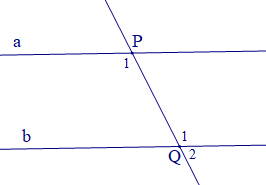
Ta có a // b nên \({\widehat P_1} = {\widehat Q_1}\) (hai góc so le trong)

Mà \({\widehat Q_1} + {\widehat {\rm{Q}}_2} = 180^\circ \) (hai góc kề bù)

Suy ra \[{\widehat {\rm{Q}}_2} = 180^\circ - {\widehat Q_1}\]

Ta lại có: \(2{\widehat {\rm{Q}}_2} - {\widehat {\rm{P}}_1} = 12^\circ \)

Suy ra \(2\left( {180^\circ - {{\widehat Q}_1}} \right) - {\widehat Q_1} = 12^\circ \)   

Hay \(360^\circ - 2{\widehat Q_1} - {\widehat Q_1} = 12^\circ \)

Do đó \(3{\widehat Q_1} = 348^\circ \)

Suy ra \({\widehat Q_1} = \frac{{348^\circ }}{3} = 116^\circ \)

Khi đó \[{\widehat {\rm{Q}}_2} = 180^\circ - {\widehat Q_1} = 180^\circ - 116^\circ = 64^\circ .\]

Vậy ta chọn phương án D.

Hướng dẫn giải:

Đáp án đúng là: C

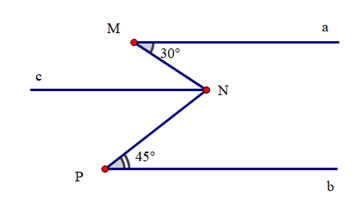
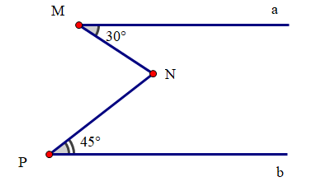
Kẻ Nc // Ma.

Suy ra \(\widehat {aMN} = \widehat {MNc} = 30^\circ \)(hai góc so le trong)

Ta có Nc // Ma, mà Ma // Pb

Suy ra Pb // Nc (vì cùng song song với Ma)

Suy ra \(\widehat {NPb} = \widehat {cNP} = 45^\circ \) (hai góc so le trong)

Ta có \(\widehat {MNP} = \widehat {MNc} + \widehat {cNP}\) (hai góc kề bù)

Do đó \(\widehat {MNP}\) = 30° + 45° = 75°.

Vậy ta chọn phương án C.