Giải SGK Toán 12 Cánh diều Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đáp án
28 người thi tuần này 4.6 1.9 K lượt thi 22 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
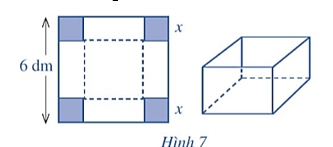
Ta thấy độ dài x (dm) của cạnh hình vuông bị cắt phải thỏa mãn điều kiện 0 < x < 3.
Từ giả thiết suy ra kích thước của khối hộp chữ nhật là x, 6 – 2x, 6 – 2x (dm).
Thể tích của khối hộp là V(x) = x(6 – 2x)2 (dm2) với 0 < x < 3.
Ta phải tìm x0 ∈ (0; 3) sao cho V(x0) có giá trị lớn nhất.
Ta có V'(x) = (6 – 2x)2 – 4x(6 – 2x) = (6 – 2x)(6 – 6x) = 12(3 – x)(1 – x).
Trên khoảng (0; 3), V'(x) = 0 khi x = 1.
Bảng biến thiên của hàm số V'(x) như sau:
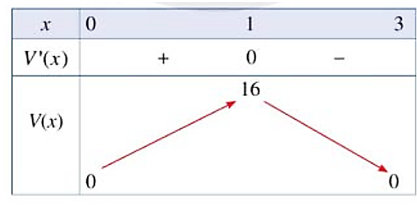
Căn cứ bảng biến thiên, ta thấy: Trên khoảng (0; 3), hàm số V(x) đạt giá trị lớn nhất bằng 16 tại x = 1.
Vậy để khối hộp tạo thành có thể tích lớn nhất thì x = 1 (dm).
Lời giải
Quan sát đồ thị Hình 8, ta thấy:
a) Điểm B(1; 3) thuộc đồ thị hàm số có tung độ lớn nhất.
b) Điểm C(0; – 1) thuộc đồ thị hàm số có tung độ nhỏ nhất.
Lời giải
Do 0 ≤ x2 ≤ 9 với mọi x ∈ [– 3; 3] nên – 9 ≤ – x2 ≤ 0 với mọi x ∈ [– 3; 3], khi đó ta suy ra 0 ≤ 9 – x2 ≤ 9 với mọi x ∈ [– 3; 3], do đó với mọi x ∈ [– 3; 3], tức là 0 ≤ f(x) ≤ 3 với mọi x ∈ [– 3; 3].
Ta có f(0) = 3 nên ; f(3) = f(– 3) = 0 nên .
Lời giải
Ta có .
a) Ta có , , x – 1 > 0 khi x → 1+.
Do đó, .
Ta có .Lời giải
b) Ta có với x > 1.
f'(x) = 0 ⇔ (x – 1)2 = 1 ⇔ x = 2 (t/m) hoặc x = 0 (loại).
Bảng biến thiên của hàm số f(x) trên khoảng (1; + ∞) như sau:
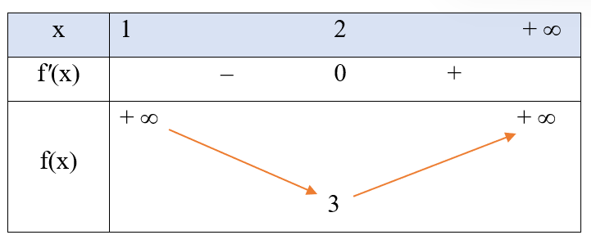
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số y = f(x) liên tục trên đoạn [– 1; 1] và có đồ thị là đường cong ở Hình 8. Quan sát đồ thị và cho biết: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/04/blobid4-1713189426.png)
![Cho hàm số y = f(x) = 2x3 – 6x, x ∈ [– 2; 2] có đồ thị là đường cong ở Hình 9. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/04/blobid1-1713191933.png)