10 Bài tập Xác định, chứng minh hai mặt phẳng song song (có lời giải)
49 người thi tuần này 4.6 527 lượt thi 10 câu hỏi 60 phút
🔥 Đề thi HOT:
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
45.6 K lượt thi
30 câu hỏi
14 Bài tập Giới hạn cực hay có lời giải chi tiết (P1)
5.2 K lượt thi
14 câu hỏi
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
8.1 K lượt thi
12 câu hỏi
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
19.6 K lượt thi
30 câu hỏi
20 câu trắc nghiệm Toán 11 Kết nối tri thức Mẫu số liệu ghép nhóm có đáp án
2.6 K lượt thi
20 câu hỏi
Bài tập Giới hạn cơ bản, nâng cao có lời giải (P1)
14.3 K lượt thi
25 câu hỏi
Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 1
1.7 K lượt thi
19 câu hỏi
Bộ 5 đề thi giữa kì 1 Toán 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
754 lượt thi
22 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. 0;
B. 1;
C. 2;
D. vô số.
Lời giải
Đáp án đúng là: A
Vì (P) và (Q) song song mà d nằm trên (P) nên d song song với (Q).
Vậy d và (Q) không có điểm chung.
Câu 2
A. (DEF) song song với (ABC);
B. (DEF) và (ABC) cắt nhau;
C. (DEF) và (ABC) trùng nhau;
D. Không thể xác định.
Lời giải
Đáp án đúng là: A
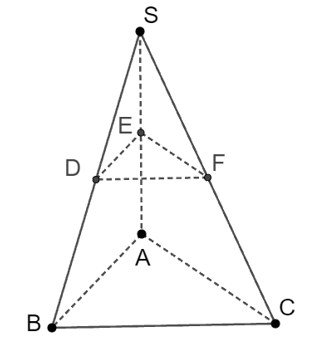
D, E, F là trung điểm các đoạn thẳng SA, SB, SC nên DE // AB, EF // AC, EF // BC (tính chất đường trung bình của tam giác).
Do đó DE, EF, EF đều song song với (ABC).
Vậy (DEF) // (ABC).
Câu 3
A. (FOE) cắt (OHE);
B. (EOF) // (SBC);
C. (HOF) ∩ (EFH) = FH;
D. (FEH) // (SBD).
Lời giải
Đáp án đúng là: B
Ta có EF là đường trung bình của tam giác SAD suy ra: EF // AD (1).
OH là đường trung bình của tam giác ABC suy ra: OH // BC // AD (2).
Từ (1) và (2) suy ra : EF // OH // AD nên 4 điểm E; F; O; H đồng phẳng
Lại có: EH // SB; OH // BC; EH, OH ⊂ (EFOH) và SB, SC ⊂ (SBC) nên (EFOH) // (SBC) hay (EOF) // (SBC).
Câu 4
A. OE // (SBC);
B. OF // (SAB);
C. (OEF) // (SBC);
D. (OEF) và (SBC) cắt nhau.
Lời giải
Đáp án đúng là: D
Câu 5
A. MN // (ABCD);
B. MP // (ABCD);
C. MP // BD;
D. (ACD) // (MNP).
Lời giải
Đáp án đúng là: C
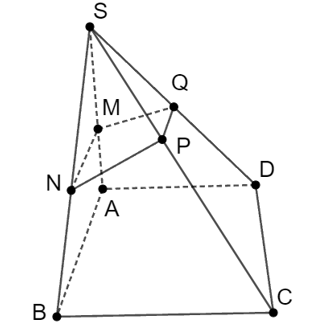
* Xét khẳng định: MN // (ABCD)
Do M và N lần lượt là trung điểm của SA và SB
⇒ MN là đường trung bình của tam giác SAB và MN // AB.
Mà AB ⊂ (ABCD) nên MN // (ABCD) (1)
⇒ A đúng.
* Xét khẳng định: MP // (ABCD).
Do M và P lần lượt là trung điểm của SA và SC
⇒ MP là đường trung bình của tam giác SAC và MP // AC
Mà AC ⊂ (ABCD) nên MP // (ABCD) (2)
⇒ B đúng.
Từ (1) và (2) và kết hợp với MN và MP là hai đường thẳng cắt nhau tại M và cùng thuộc (MNPQ) ta suy ra: (ABCD) // (MNPQ)
⇒ D đúng.
Vậy khẳng định sai là C.
Câu 6
A. Cắt nhau;
B. Song song;
C. Trùng nhau;
D. Không thể xác định.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Song song;
B. Cắt nhau;
C. Trùng nhau;
D. Không thể xác định.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. SI = 2IC;
B. SI = 3IC;
C. SI = IC;
D. SI = 4IC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. GM;
B. HM;
C. GH;
D. GS.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. Song song;
B. Cắt nhau;
C. Trùng nhau;
D. Không xác định được.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập