10 Bài tập Tìm và chứng minh hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh từ đó chứng minh tính chất khác (có lời giải)
32 người thi tuần này 4.6 190 lượt thi 10 câu hỏi 60 phút
🔥 Đề thi HOT:
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
21.1 K lượt thi
17 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
16.8 K lượt thi
17 câu hỏi
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
14.3 K lượt thi
15 câu hỏi
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
5.7 K lượt thi
23 câu hỏi
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
6 K lượt thi
30 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
16.1 K lượt thi
29 câu hỏi
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
5.8 K lượt thi
21 câu hỏi
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02
5.2 K lượt thi
23 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: B
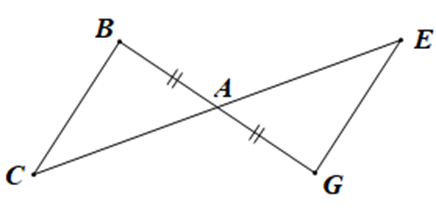
Vì DABC = DDEG theo trường hợp cạnh – góc – cạnh nên điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.
Mà \(\widehat {ABC}\) là góc xen kẽ giữa hai cạnh BA và BC, \(\widehat {DEG}\) là góc xen kẽ giữa hai cạnh ED và EG.
Lại có BA = ED
Do đó điều kiện còn lại là điều kiện về cạnh, đó là BC = EG.
Ta chọn phương án B.
Lời giải
Đáp án đúng là: C
Vì DABC = DAGE theo trường hợp cạnh – góc – cạnh nên điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.
Mà \(\widehat {BAC} = \widehat {GAE}\) (hai góc đối đỉnh)
Góc BAC xen kẽ giữa hai cạnh AB và AC, góc GAE xen kẽ giữa hai cạnh AG và AE.
Mà AB = AG nên điều kiện còn thiếu trong trường hợp này là điều kiện về cạnh, đó là AC = AE.
Vậy ta chọn phương án C.
Lời giải
Đáp án đúng là: C
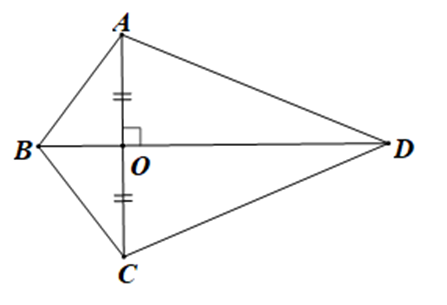
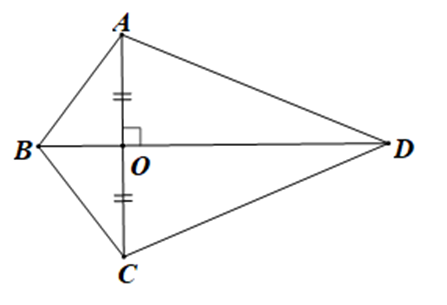
+ Xét tam giác ABO và tam giác CBO có:
AO = CO, \(\widehat {AOB} = \widehat {COB}\left( { = 90^\circ } \right),\) BO là cạnh chung
Do đó DABO = DCBO (c.g.c)
+ Xét DAOD và DCOD có:
AO = CO, \(\widehat {AOD} = \widehat {COD}\left( { = 90^\circ } \right),\) OD là cạnh chung
Do đó D AOD = DCOD (c.g.c)
+ Vì DABO = DCBO (chứng minh trên)
Nên (hai góc tương ứng) và AB = CB (hai cạnh tương ứng)
Xét DABD và DCBD có:
AB = CB (chứng minh trên);
(do )
BD là cạnh chung
Do đó DABD = DCBD (c.g.c)
Vậy có 3 cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.
Lời giải
Đáp án đúng là: A
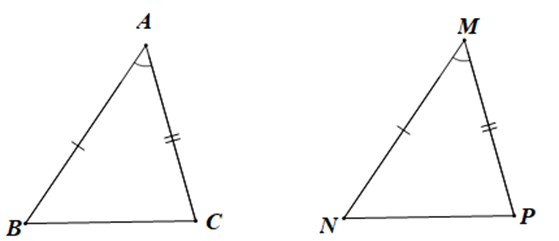
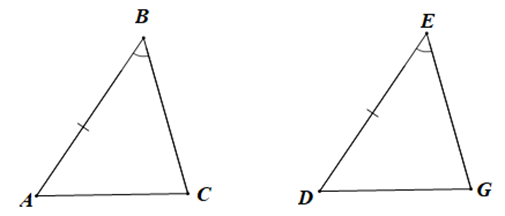
Xét DBAC và DMNP có:
BA = MN (giả thiết),
(giả thiết),
CA = MP (giả thiết)
Do đó DBAC = DNMP (c.g.c)
Vậy ta chọn phương án A.
Lời giải
Đáp án đúng là: C
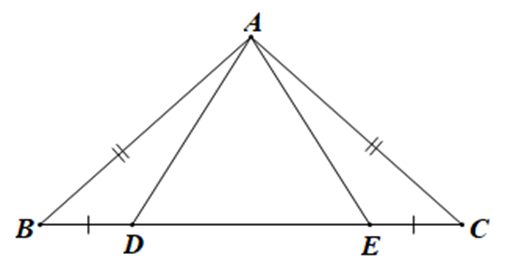
+ Xét DABD và DACE có:
AB = AC (giả thiết),
(giả thiết),
BD = CE (giả thiết)
Do đó DABD = DACE (c.g.c)
+ Vì BE = BD + DE, CD = CE + ED
Mà BD = CE (giả thiết) nên BE = CD.
Xét DABE và DACD có:
AB = AC (giả thiết),
(giả thiết),
BE = CD (chứng minh trên)
Do đó DABE = DACD (c.g.c)
Vậy cả phương án A và B đều đúng, ta chọn phương án C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
4.6
38 Đánh giá
50%
40%
0%
0%
0%