10 Bài tập Nhận biết và chứng minh tam giác cân, tam giác đều (có lời giải)
44 người thi tuần này 4.6 441 lượt thi 10 câu hỏi 60 phút
🔥 Đề thi HOT:
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
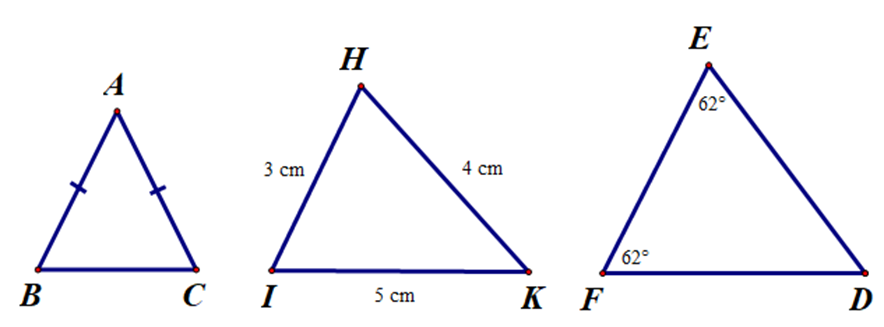
Xét ∆ABC có: AB = AC (giả thiết).
Suy ra ∆ABC cân tại A.
Xét ∆HIK có: HI ≠ IK ≠ HK (vì 3 cm ≠ 5 cm ≠ 4 cm).
Do đó ∆HIK không phải là tam giác cân.
Xét ∆DEF có: \[\widehat {DEF} = \widehat {DFE} = 62^\circ \].
Suy ra ∆DEF cân tại D.
Khi đó hình trên có 2 tam giác cân là: ∆ABC và ∆DEF.
Vậy ta chọn đáp án C.
Lời giải
Đáp án đúng là: C
Đáp án A, B, D đúng.
Đáp án C sai. Sửa lại:
Cách sửa 1: Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có hai góc bằng 60°;
Cách sửa 2: Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó là một tam giác cân và có một góc bằng 60°.
Vậy ta chọn đáp án C.
Lời giải
Đáp án đúng là: A
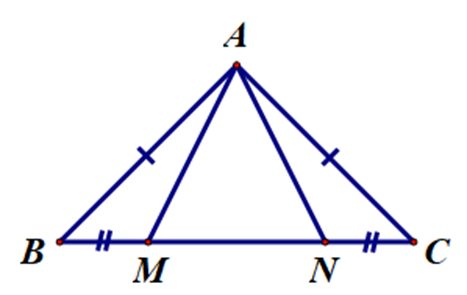
Vì ∆ABC cân tại A nên ta có AB = AC và \[\widehat {ABC} = \widehat {ACB}\].
Xét ∆ABM và ∆ACN, có:
AB = AC (chứng minh trên).
\[\widehat {ABC} = \widehat {ACB}\] (chứng minh trên).
BM = CN (giả thiết).
Do đó ∆ABM = ∆ACN (cạnh – góc – cạnh).
Suy ra AM = AN (cặp cạnh tương ứng).
Do đó ∆AMN cân tại A.
Vậy ta chọn đáp án A.
Lời giải
Đáp án đúng là: D
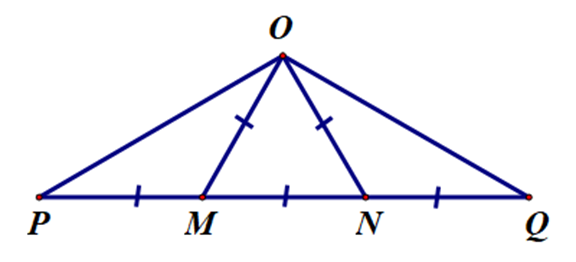
Quan sát hình, ta thấy OM = ON = MN.
Do đó ∆OMN là tam giác đều.
Quan sát hình, ta thấy OM = PM.
Do đó ∆OPM là tam giác cân tại M.
Quan sát hình, ta thấy ON = NQ.
Do đó ∆ONQ là tam giác cân tại N.
Khi đó ta có: ∆OMN là tam giác đều; ∆OPM và ∆ONQ là các tam giác cân.
Do đó đáp án B, C đều đúng.
Vậy ta chọn đáp án D.
Lời giải
Đáp án đúng là: D
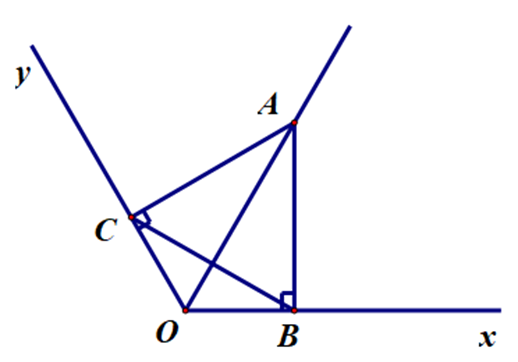
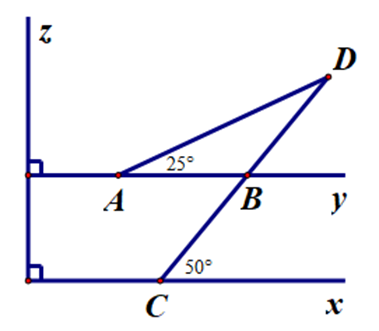
Xét ∆OAB và ∆OAC, có:
\[\widehat {ACO} = \widehat {ABO} = 90^\circ \].
OA là cạnh chung.
\[\widehat {AOC} = \widehat {AOB}\] (OA là phân giác của \[\widehat {xOy}\]).
Do đó ∆OAB = ∆OAC (cạnh huyền – góc nhọn).
Suy ra AB = AC (cặp cạnh tương ứng).
Do đó ∆ABC cân tại A (1).
Ta có OA là phân giác của \[\widehat {xOy}\].
Suy ra \[\widehat {BOA} = \widehat {AOC} = \frac{{120^\circ }}{2} = 60^\circ \].
∆OAB vuông tại B: \[\widehat {BOA} + \widehat {OAB} = 90^\circ \].
Suy ra \[\widehat {OAB} = 90^\circ - \widehat {BOA} = 90^\circ - 60^\circ = 30^\circ \].
Chứng minh tương tự, ta được \[\widehat {OAC} = 30^\circ \].
Do đó ta có \[\widehat {OAB} + \widehat {OAC} = 30^\circ + 30^\circ = 60^\circ \].
Ta suy ra \[\widehat {BAC} = 60^\circ \] (2).
Từ (1), (2), ta suy ra ∆ABC là tam giác đều.
Vậy ta chọn đáp án D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
88 Đánh giá
50%
40%
0%
0%
0%