Bết đồ thị hàm số (m, n là tham số) nhận trục hoành và trục tung làm hai đường tiệm cận. Tính m + n.
A. -6.
B. 9.
C. 6.
D. 8.
Quảng cáo
Trả lời:
Chọn B.
Ta có
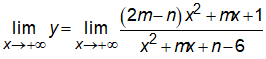
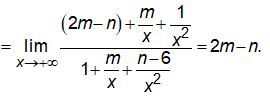
Tương tự, ta cũng có
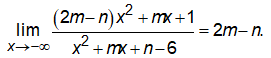
Vậy y = 2m – n là đường tiệm cận ngang của đồ thị hàm số.
Theo giả thiết, ta có 2m – n = 0 (1).
Để hàm số nhận trục tung làm tiệm cận đứng thì điều kiện cần là phương trình ![]() có một nghiệm x = 0 hay n - 6 = 0 n = 6 (2)
có một nghiệm x = 0 hay n - 6 = 0 n = 6 (2)
Do x = 0 không là nghiệm của phương trình![]() nên với n = 6 thì đồ thị hàm số nhận trục tung làm tiệm cận đứng.
nên với n = 6 thì đồ thị hàm số nhận trục tung làm tiệm cận đứng.
Từ (1) và (2) suy ra m = 3. Vậy m + n = 9.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 4 máy.
B. 6 máy.
C. 5 máy.
D. 7 máy.
Lời giải
Chọn C.
Gọi ![]() là số máy in sử dụng trong một giờ để được lãi nhiều nhất. Khi đó chi phí dành cho x máy in trong một giờ là nghìn đồng.
là số máy in sử dụng trong một giờ để được lãi nhiều nhất. Khi đó chi phí dành cho x máy in trong một giờ là nghìn đồng.
Chi phí vận hành 50x nghìn đồng.
Số bản in trong một giờ là 3600x => thời gian để in xong 50000 tờ quảng cáo là ![]()
Vậy tổng chi phí là ![]() nghìn đồng
nghìn đồng
Để lãi là nhiều nhất thì tổng chi phí là thấp nhất, vậy ta tìm giá trị nhỏ nhất của tổng chi phí.
Thay các giá trị x = {1;2;3;4;5;6;7;8} ta thấy giá trị nhỏ nhất là ![]()
Câu 2
A. |x-2y| = 10
B. |x-2y| = 9
C. |x-2y| = 6
D. |x-2y| = 8
Lời giải
Chọn C.
Theo tính chất của cấp số cộng và cấp số nhân ta có
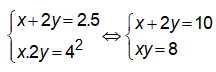
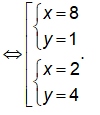
Vậy |x-2y| = 6
Câu 3
Tìm tất cả các giá trị của m để đồ thị hàm số y = chỉ có một điểm cực đại và không có điểm cực tiểu.
A. -1,5 < m 0
B. m 1
C. -1 m 0
D. -1 < m < 0,5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. y = 2
B. y =
C. y = 4
D. y = -2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. m < 0.
B. m > 1.
C. m 1
D. m 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.