Bộ 10 đề thi Giữa kì 2 Toán 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 6
24 người thi tuần này 4.6 4.2 K lượt thi 5 câu hỏi 60 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
19 câu Trắc nghiệm Toán 7 Bài 6: Tam giác cân có đáp án (Vận dụng)
5 câu Trắc nghiệm Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu có đáp án (Nhận biết)
9 câu Trắc nghiệm Toán 7 Bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc có đáp án (Thông hiểu)
5 câu Trắc nghiệm Toán 7 Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác có đáp án (Nhận biết)
5 câu Trắc nghiệm Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng có đáp án (Nhận biết)
9 câu Trắc nghiệm Toán 7 Bài 7: Định lí Pi-ta-go có đáp án (Vận dụng)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
a) \(\frac{{1,2}}{{x + 3}} = \frac{5}{4}\) nên \(5\left( {x + 3} \right) = 4.1,2\) hay \(5x + 15 = 4,8\), do đó \(5x = 4,8 - 15\) được \(5x = 10,2\).
Suy ra \(x = 2,04\).
Vậy \(x = 2,04\).
b) \(\frac{x}{8} = \frac{y}{{12}}\) và \(x + y = 60\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{x}{8} = \frac{y}{{12}} = \frac{{x + y}}{{8 + 12}} = \frac{{60}}{{20}} = 3\).
Suy ra \(\frac{x}{8} = 3\) nên \(x = 24\) và \(\frac{y}{{12}} = 3\) nên \(y = 36\).
Vậy \(x = 24\) và \(y = 36\).
c) \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\) và \(x + y + z = 30\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5} = \frac{{x + y + z}}{{2 + 3 + 5}} = \frac{{30}}{{10}} = 3\).
Suy ra \(x = 2.3 = 6;{\rm{ }}y = 3.3 = 9;{\rm{ }}z = 5.3 = 15\).
Vậy \(x = 6;y = 9;z = 15\).
Lời giải
Hướng dẫn giải
a) Từ bảng trên, ta thấy với \(x = 7\) thì \(y = - 8\) và \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch nên ta có hệ số tỉ lệ \(a = xy = 7.\left( { - 8} \right) = - 56\).
Suy ra \(y = \frac{{ - 56}}{x}\) hay hệ số tỉ lệ của \(y\) đối với \(x\) là \( - 56.\)
b) Ta có hệ số tỉ lệ \(a = - 56\) nên ta được:

Lời giải
Hướng dẫn giải
3.1.Gọi thời gian để 5 máy cày cày xong cánh đồng là \[x\] giờ \[\left( {x > 0} \right)\].
Vì năng suất của mỗi máy cày là như nhau nên để cày cùng một cánh đồng, số máy cày tỉ lệ nghịch với số giờ cày xong cánh đồng.
Theo tính chất của đại lượng tỉ lệ nghịch, ta có: \[\frac{{30}}{x} = \frac{5}{3}\] do đó, \[x = \frac{{3.30}}{5} = 18\].
Vậy 5 máy cày cày xong cánh đồng đó hết 18 giờ.
3.2.Gọi chiều dài của ba cuộn vải loại \(I,\) loại \(II,\) loại \(III\) lần lượt là \(a,b,c{\rm{ }}\left( {\rm{m}} \right)\) với \(\left( {0 < a,b,c < 168} \right)\).
Sau một ngày, cửa hàng bán được số vải của các cuộn là
Cuộn vải loại \(I\) bán được: \(a - \frac{2}{3}a = \frac{1}{3}a{\rm{ }}\left( {\rm{m}} \right)\).
Cuộn vải loại \(II\) bán được: \(b - \frac{1}{3}b = \frac{2}{3}b{\rm{ }}\left( {\rm{m}} \right)\).
Cuộn vải loại \(III\) bán được: \(c - \frac{3}{5}c = \frac{2}{5}c{\rm{ }}\left( {\rm{m}} \right)\).
Do giá tiền \(1{\rm{ m}}\) vải của các cuộn bằng nhau nên số mét vải bán được của các cuộn tỉ lệ với số tiền bán được, mà số tiền bán được của các cuộn tỉ lệ với \(2:3:2\). Do đó, số vải bán được của các cuộn tỉ lệ với \(2:3:2\).
Ta có: \(\frac{{\frac{1}{3}a}}{2} = \frac{{\frac{2}{3}b}}{3} = \frac{{\frac{2}{5}c}}{2}\) suy ra \(\frac{a}{6} = \frac{{2b}}{9} = \frac{{2c}}{{10}}\) suy ra \(\frac{a}{6} = \frac{b}{{4,5}} = \frac{c}{5}\).
Mà tổng chiều dài của ba cuộn vải là \(186{\rm{ m}}\) nên \(a + b + c = 186{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{6} = \frac{b}{{4,5}} = \frac{c}{5} = \frac{{a + b + c}}{{6 + 4,5 + 5}} = \frac{{186}}{{15,5}} = 12\).
Suy ra \(\frac{a}{6} = 12\) nên \(a = 72{\rm{ m}}{\rm{.}}\)
\(\frac{b}{{4,5}} = 12\) nên \(b = 54{\rm{ m}}\).
\(\frac{c}{5} = 12\) nên \(c = 60{\rm{ m}}{\rm{.}}\)
Vậy chiều dài của ba cuộn vải loại \(I,\) loại \(II,\) loại \(III\) lần lượt là \(72{\rm{ m, 54 m, 60 m}}{\rm{.}}\)
Lời giải
Hướng dẫn giải
Gọi ba chữ số hàng trăm, hàng chục và hàng đơn vị của số cần tìm lần lượt là \(a,b,c\).
Điều kiện: \(a,b,c \in \mathbb{N}\) và \(a \ne 0\).
Theo đề, các chữ số tỉ lệ với ba số \(1;2;3\) nên ta có: \(\frac{a}{1} = \frac{b}{2} = \frac{c}{3} = \frac{{a + b + c}}{{1 + 2 + 3}} = \frac{{a + b + c}}{6}\) (1)
Do đó, \(\left( {a + b + c} \right) \vdots 6\), mặt khác số đó chia hết cho 18 nên số đó chia hết cho \(9\).
Suy ra \(\left( {a + b + c} \right) \vdots 9\) mà có \(0 < a + b + c \le 9 + 9 + 9\) hay \(0 < a + b + c \le 27\).
Do đó, \(a + b + c = 18\) (2)
Từ (1) và (2) suy ra \(\frac{a}{1} = \frac{b}{2} = \frac{c}{3} = \frac{{a + b + c}}{{1 + 2 + 3}} = \frac{{a + b + c}}{6} = \frac{{18}}{6} = 3\).
Do đó, \(a = 3,b = 6,c = 9\).
Vậy số cần tìm là \(369\).
Lời giải
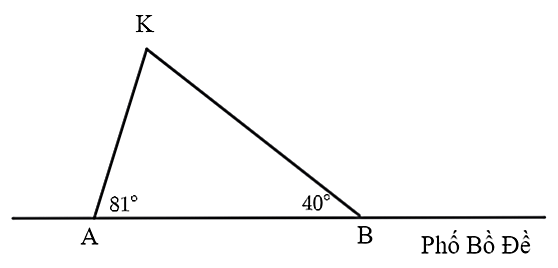
4.1.Từ hình vẽ minh họa, xét \(\Delta ABK\), ta có:
\(\widehat A > \widehat B{\rm{ }}\left( {81^\circ > 40^\circ } \right)\), do đó \(KB > KA\) (tính chất của góc và cạnh đối diện trong tam giác).
Vì vậy bạn Cường nên xuống xe ở điểm \(A\) rồi đi bộ đến trường để quãng đường ngắn nhất.
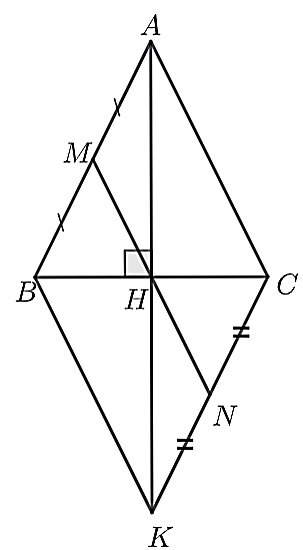
4.2. a) Xét \(\Delta ABH\) và \(\Delta ACH\), có:
\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))
\(AH\): chung (gt)
\(\widehat {AHB} = \widehat {AHC} = 90^\circ \) (gt)
Do đó, \(\Delta ABH = \Delta ACH\) (ch – gn).
b) Xét \(\Delta BHK\) và \(\Delta CHA\), có:
\(BH = HC\) (gt)
\(\widehat {BHK} = \widehat {CHA} = 90^\circ \) (đối đỉnh)
\(HA = HK\) (gt)
Do đó, \(\Delta BHK = \Delta CHA\) (c.g.c)
Suy ra \(\widehat {KBH} = \widehat {HCA}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong, suy ra \(AC\parallel BK.\)
c) Xét \(\Delta ABH\) và \(\Delta CHK\), có:
\(HB = HC\) (hai cạnh tương ứng)
\(AH = HK\) (gt)
(đối đỉnh)
Do đó, \(\Delta ABH = \Delta CHK\) (c.g.c)
Suy ra \(\widehat {BAH} = \widehat {HKC}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong nên \(AB\parallel KC\).
Lại có \(AB = KC\) (hai cạnh tương ứng).
Mà \(M,N\) là trung điểm của \(AB,CK\). Do đó, \(AM = KN\)
Xét \(\Delta MAH\) và \(\Delta NKH\), có:
\(AM = KN\) (cmt)
\(\widehat {BAH} = \widehat {HKC}\) (cmt)
\(AH = HK\) (gt)
Do đó, \(\Delta MAH = \Delta NKH\) (c.g.c)
Suy ra \(\widehat {MHA} = \widehat {NHK}\) (hai góc tương ứng).
Mà hai góc ở vị trí đối đỉnh, do đó \(M,H,N\) thẳng hàng.