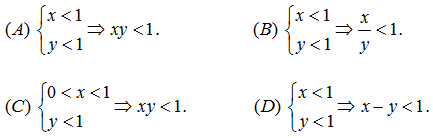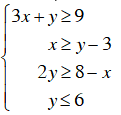Ôn tập chương 4
17 người thi tuần này 4.6 11.6 K lượt thi 14 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) -Đề 3
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) -Đề 2
Đề kiểm tra Đường tròn trong mặt phẳng toạ độ (có lời giải) - Đề 1
Đề kiểm tra Vị trí tương đối giữa hai đường thẳng.góc và khoảng cách (có lời giải) - Đề 3
Đề kiểm tra Vị trí tương đối giữa hai đường thẳng.góc và khoảng cách (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
a) x > 0
b) y ≥ 0
c) ∀α ∈ R, |α| ≥ 0
d) ∀a, b > 0,
Lời giải
a) Hai số a và b cùng dấu.
b) Hai số a và b cùng dấu.
c) Hai số a và b trái dấu nhau.
d) Hai số a và b trái dấu nhau.
Lời giải
Suy luận (C) đúng.
Giải thích:
+ Suy luận (A) sai.
Ví dụ: x = y = –2 < 1 thì x.y = 4 > 1.
+ Suy luận (B) sai
Ví dụ : x = –6 < 1, y = –3 < 1 thì (x/y) = 2 > 1.
+ Suy luận (C) đúng vì
Nếu 0 < y < 1 và 0 < x < 1 thì x.y < 1.1 = 1 (Nhân hai BĐT cùng chiều)
Nếu y ≤ 0 và 0 < x < 1 thì x.y ≤ 0 (Do x và y trái dấu) nên x.y < 1.
Do đó với mọi x, y thỏa mãn 0 < x < 1 và y < 1 ⇒ xy < 1.
+ Suy luận (D) sai
Ví dụ: x = 0 < 1, y = -5 < 1 thì x - y = 5 > 1.
Lời giải
Khối lượng thực của vật nằm trong khoảng (26,4 - 0,05; 26,4 + 0,05) = (26,35; 26,45) kg.
Lời giải
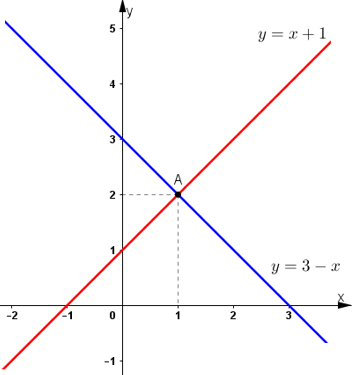
Vẽ đồ thị:
- Vẽ đồ thị hàm số y = f(x) = x + 1 qua hai điểm (0; 1) và (-1; 0).
- Vẽ đồ thị hàm số y = g(x) = 3 - x qua hai điểm (0; 3) và (3; 0)
a) Nghiệm của phương trình f(x) = g(x) chính là hoành độ giao điểm của hai đường thẳng y = f(x) và y = g(x).
Giao điểm của hai đường thẳng y = x + 1 và y = 3 – x là điểm A(1; 2).
Do đó phương trình f(x) = g(x) có nghiệm x = 1.
Kiểm tra bằng tính toán:
f(x) = g(x) ⇔ x + 1 = 3 - x ⇔ 2x = 2 ⇔ x = 1.
b) Khi x > 1 thì đồ thị hàm số y = f(x) nằm phía trên đồ thị hàm số y = g(x), hay với x > 1 thì f(x) > g(x).
Kiểm tra bằng tính toán:
f(x) > g(x) ⇔ x + 1 > 3 - x ⇔ 2x > 2 ⇔ x > 1.
c) Khi x < 1 thì đồ thị hàm số y = f(x) nằm phía dưới đồ thị hàm số y = g(x), hay với x < 1 thì f(x) < g(x).
Kiểm tra bằng tính toán:
f(x) < g(x) ⇔ x + 1 < 3 - x ⇔ 2x < 2 ⇔ x < 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
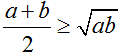
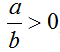 ;
;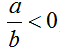 ?
?