10 Bài tập Tính giá trị của biểu thức liên quan đến các giá trị lượng giác (có lời giải)
80 người thi tuần này 4.6 1.3 K lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 8
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 7
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 6
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 5
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 2
Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 1
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Thay x = 30° vào biểu thức A ta có:
A = sin (2.30°) – 3cos 30° = sin 60° – 3cos 30° = – 3. = – .
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có: α + β = π ⇒ α = π – β.
Do đó A = sin2 (π – β) + cos2 (π – α) = (sin α)2 + (– cos α)2 = sin2 α + cos2 α = 1.
Câu 3
A. 2;
B. 1;
C. 3;
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Ta có: sin2 x + cos2 x = 1 ⇒ cos2 x = 1 – sin2 x = .
Do đó A = . + = .
Như vậy a = 49, b = 48 ⇒ a – b = 1.
Lời giải
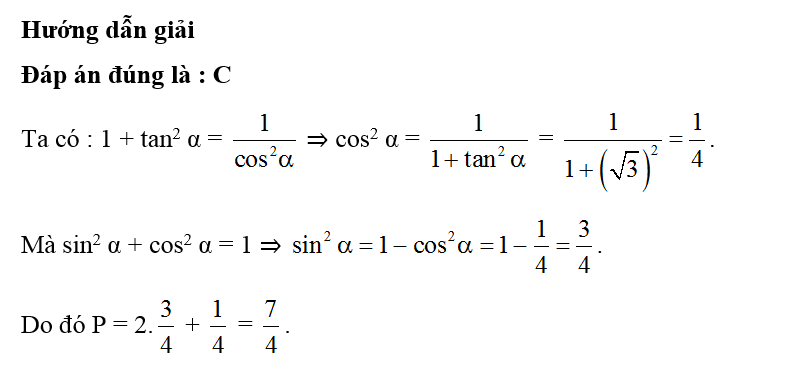
Lời giải

Câu 6
A. 4sin2 α + 2cos2 α = 3;
B. 4sin2 α + 2cos2 α = – 3;
C. 4sin α + 2cos α = ;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 52;
B. 35;
C. 34;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 9;
B. 8;
C. 7;
D. 23.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.