10 Bài tập Thể tích khối chóp, khối chóp cụt đều (có lời giải)
42 người thi tuần này 4.6 756 lượt thi 10 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
Bài tập Giới hạn cơ bản, nâng cao có lời giải (P1)
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P3)
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P2)
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
20 câu trắc nghiệm Toán 11 Kết nối tri thức Mẫu số liệu ghép nhóm có đáp án
20 câu Trắc nghiệm Toán 11 Cánh diều Bài 4. Hai mặt phẳng song song (Đúng-sai, trả lời ngắn) có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
Lời giải
Đáp án đúng là: C
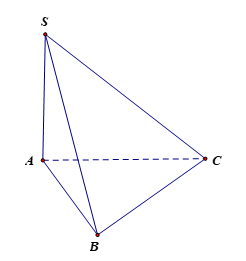
Vì AB2 + AC2 = BC2 (62 + 82 = 102) nên DABC vuông tại A.
Khi đó .
Do đó .
Lời giải
Đáp án đúng là: B
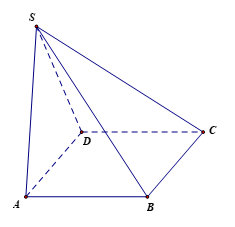
Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với (ABCD), suy ra SA ^ (ABCD). Do đó chiều cao khối chóp là .
Diện tích hình chữ nhật ABCD là SABCD = AB.BC = 2a2.
Vậy thể tích khối chóp
Lời giải
Đáp án đúng là: A
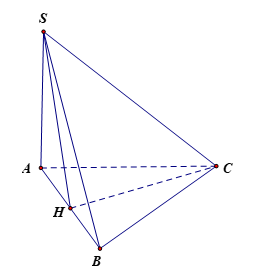
Gọi H là trung điểm của AB, suy ra SH ^ AB (do DSAB đều).
Do (SAB) ^ (ABC) theo giao tuyến AB nên SH ^ (ABC).
Tam giác SAB là đều cạnh a nên .
Tam giác vuông ABC, có .
Diện tích tam giác vuông .
Vậy .
Lời giải
Đáp án đúng là: B
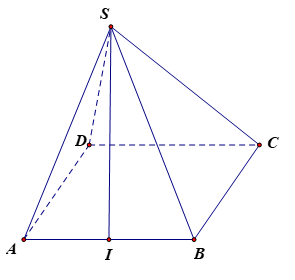
Gọi I là trung điểm của AB.
Tam giác SAB cân tại S và có I là trung điểm AB nên SI ^ AB.
Do (SAB) ^ (ABCD) theo giao tuyến AB nên SI ^ (ABCD).
Tam giác vuông SIA, có
Diện tích hình vuông ABCD là SABCD = a2.
Vậy
Lời giải
Đáp án đúng là: B
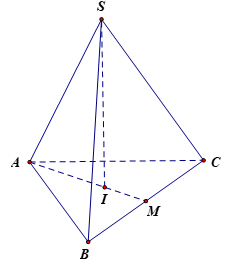
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC.
Vì S.ABC là khối chóp đều nên suy ra SI ^ (ABC).
Gọi M là trung điểm của BC.
Vì DABC đều nên
Tam giác SAI vuông tại I, có
Diện tích tam giác ABC là
Vậy thể tích khối chóp
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.