10 Bài tập Vận dụng định nghĩa, tính chất của tam giác cân để chứng minh tính chất khác (có lời giải)
31 người thi tuần này 4.6 191 lượt thi 10 câu hỏi 60 phút
🔥 Đề thi HOT:
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: D
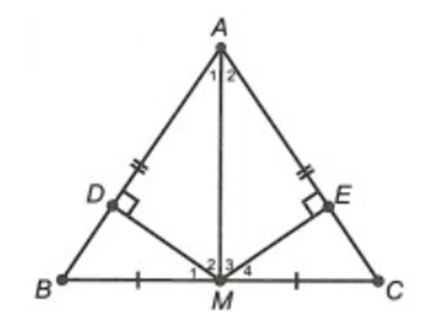
Xét ∆BDM và ∆CEM, có:
\[\widehat {BDM} = \widehat {CEM} = 90^\circ \].
\[\widehat {DBM} = \widehat {ECM}\] (∆ABC cân tại A).
MB = MC (M là trung điểm BC).
Do đó ∆BDM = ∆CEM (cạnh huyền – góc nhọn).
Suy ra BD = CE và \[\widehat {BMD} = \widehat {CME}\] (cặp cạnh và cặp góc tương ứng).
Do đó đáp án A, C đúng.
Xét ∆ADM và ∆AEM, có:
\[\widehat {ADM} = \widehat {AEM} = 90^\circ \].
AM là cạnh chung.
DM = EM (∆BDM = ∆CEM).
Do đó ∆ADM = ∆AEM (cạnh huyền – cạnh góc vuông).
Suy ra AD = AE (cặp cạnh tương ứng).
Do đó đáp án B đúng.
Vậy ta chọn đáp án D.
Lời giải
Đáp án đúng là: B
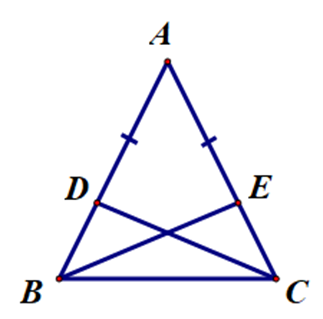
Ta xét từng đáp án:
+ Đáp án B, D:
Vì ∆ABC cân tại A nên ta có AB = AC và \[\widehat {ABC} = \widehat {ACB}\].
Xét ∆ABE và ∆ACD, có:
\[\widehat {BAC}\] là góc chung.
AB = AC (chứng minh trên).
AD = AE (giả thiết).
Do đó ∆ABE = ∆ACD (cạnh – góc – cạnh).
Suy ra BE = CD và \[\widehat {ABE} = \widehat {ACD}\] (cặp cạnh và cặp góc tương ứng).
Do đó đáp án B đúng, đáp án D sai.
Đến đây ta có thể chọn đáp án B.
+ Đáp án C:
Ta có A, D, B thẳng hàng. Suy ra BD = AB – AD.
Ta có A, E, C thẳng hàng. Suy ra EC = AC – AE.
Ta có AB = AC (chứng minh trên) và AD = AE (giả thiết).
Suy ra AB – AD = AC – AE.
Do đó BD = EC.
Do đó đáp án C sai.
+ Đáp án A:
Xét ∆BDC và ∆CEB, có:
BC là cạnh chung.
BD = EC (chứng minh trên).
\[\widehat {DBC} = \widehat {ECB}\] (chứng minh trên).
Do đó ∆BDC = ∆CEB (cạnh – góc – cạnh).
Suy ra \[\widehat {BDC} = \widehat {CEB}\] (cặp góc tương ứng).
Do đó đáp án A sai.
Vậy ta chọn đáp án B.
Lời giải
Đáp án đúng là: D
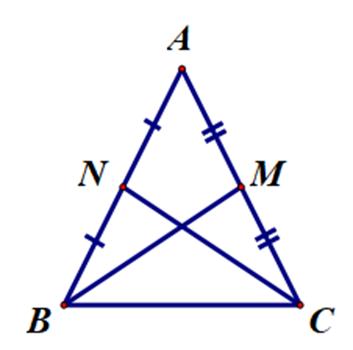
Ta có M là trung điểm AC (giả thiết).
Do đó AC = 2AM = 2CM (1).
Ta có N là trung điểm AB (giả thiết).
Do đó AB = 2AN = 2BN (2).
Vì ∆ABC cân tại A nên AB = AC (3).
Từ (1), (2), (3), ta suy ra AM = AN = CM = BN.
Xét ∆ABM và ∆ACN, có:
AB = AC (∆ABC cân tại A).
\[\widehat {BAC}\] là góc chung.
AM = AN (chứng minh trên).
Do đó ∆ABM = ∆ACN (cạnh – góc – cạnh).
Suy ra (I) đúng.
Xét ∆BMC và ∆CNB, có:
BC là cạnh chung.
CM = BN (chứng minh trên).
\[\widehat {NBC} = \widehat {MBC}\] (∆ABC cân tại A).
Do đó ∆BMC = ∆CNB (cạnh – góc – cạnh).
Suy ra (II) đúng.
Vậy ta chọn đáp án D.
Lời giải
Đáp án đúng là: A
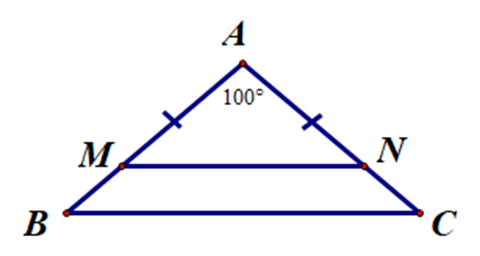
Vì AM = AN nên ∆AMN cân tại A.
Suy ra \[\widehat {AMN} = \widehat {ANM}\].
Do đó đáp án D sai.
Xét ∆AMN, có: \[\widehat {MAN} + \widehat {AMN} + \widehat {ANM} = 180^\circ \].
Suy ra \[2\widehat {AMN} = 180^\circ - \widehat {MAN} = 180^\circ - 100^\circ = 80^\circ \].
Do đó \[\widehat {AMN} = 40^\circ \].
Xét ∆ABC, có: \[\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \].
Suy ra \[2\widehat {ABC} = 180^\circ - \widehat {BAC} = 180^\circ - 100^\circ = 80^\circ \].
Do đó \[\widehat {ABC} = 40^\circ \].
Ta suy ra \[\widehat {AMN} = \widehat {ABC} = 40^\circ \].
Mà hai góc này ở vị trí đồng vị.
Suy ra MN // BC.
Do đó đáp án A đúng.
Vì ba điểm A, B, C tạo thành một tam giác và MN // BC.
Nên MN không song song với AB và MN không song song với AC.
Do đó đáp án B, C sai.
Vậy ta chọn đáp án A.
Lời giải
Đáp án đúng là: C
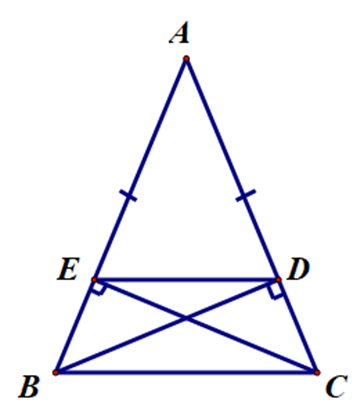
Vì ∆ABC cân tại A nên AB = AC.
Mà AE = AD (giả thiết).
Do đó AB – AE = AC – AD.
Suy ra EB = DC.
Xét ∆CBE và ∆BCD, có:
BC là cạnh chung.
EB = DC (chứng minh trên).
\[\widehat {EBC} = \widehat {DCB}\] (∆ABC cân tại A).
Do đó ∆CBE = ∆BCD (cạnh – góc – cạnh).
Suy ra \[\widehat {CEB} = \widehat {BDC} = 90^\circ \] (cặp góc tương ứng).
Khi đó ta có CE ⊥ BE hay CE ⊥ AB.
Do đó đáp án C đúng.
Vì A, B, C tạo thành một tam giác và CE ⊥ AB.
Nên CE không vuông góc với BC và CE không vuông góc với AC.
Do đó đáp án B, D sai.
∆ADE có AE = AD.
Suy ra ∆ADE cân tại A.
Do đó \[\widehat {AED} = \widehat {ADE}\].
∆ADE có: \[\widehat {BAC} + \widehat {AED} + \widehat {ADE} = 180^\circ \].
Suy ra \[2\widehat {AED} = 180^\circ - \widehat {BAC}\] (1).
∆ABC có: \[\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \].
Suy ra \[2\widehat {ABC} = 180^\circ - \widehat {BAC}\] (2).
Từ (1), (2), ta suy ra \[\widehat {AED} = \widehat {ABC}\].
Mà hai góc này ở vị trí đồng vị.
Do đó DE // BC.
Suy ra đáp án A sai.
Vậy ta chọn đáp án C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
38 Đánh giá
50%
40%
0%
0%
0%