Câu hỏi:

13/02/2020 29,881

Cho hàm số y = ${(x^{3} - 3 x + m)}^{2}$ . Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn [-1;1] bằng 1 là

A. 1

B. -4

C. 0

D. 4

Xem lời giải

Câu hỏi trong đề: 220 Bài trắc nghiệm Hàm số từ đề thi thử THPTQG 2019 cực hay có lời giải chi tiết !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn C

Xét hàm số f(x) = $x^{3} - 3 x + m$ .

Để GTNN của hàm số y = ${(x^{3} - 3 x + m)}^{2}$ trên đoạn [-1;1] bằng 1 thì hoặc

Ta có

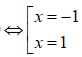
=> f(x) nghịch biến trên [-1;1]

Suy ra và

Trường hợp 1:

Trường hợp 2:

Vậy tổng các giá trị của tham số m là 0.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

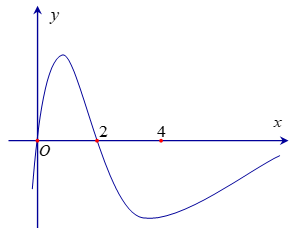
Câu 1

Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)

B. m = f(1), M = f(2)

C. m = f(4), M = f(1)

D. m = f(0), M = f(2)

Lời giải

Chọn A

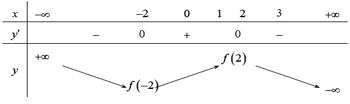
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.

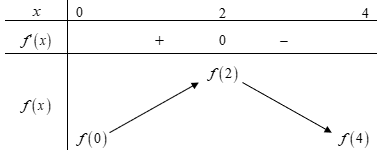
Vậy giá trị lớn nhất M = f(2)

Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .

Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.

Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).

=> f(0) > f(4)

Vậy giá trị nhỏ nhất m = f(4)

Câu 2

Cho hàm số y = $a x^{3} + c x + d, a \neq 0$ có $\underset{x \in (- \infty; 0)}{m i n} f (x) = f (- 2)$ . Giá trị lớn nhất của hàm số y = f(x) trên đoạn [1;3] bằng

A. d - 11a

B. d - 16a

C. d + 2a

D. d + 8a

Lời giải

Chọn B

Vì y = $a x^{3} + c x + d, a \neq 0$ là hàm số bậc ba và có $\underset{x \in (- \infty; 0)}{m i n} f (x) = f (- 2)$ nên a < 0 và y' = 0 có hai nghiệm phân biệt.

Ta có có hai nghiệm phân biệt $\Leftrightarrow$ ac < 0

Vậy với a < 0, c > 0 thì y' = 0 có hai nghiệm đối nhau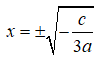

Từ đó suy ra

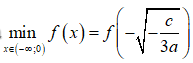
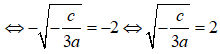
$\Leftrightarrow$ c = -12a

Ta có bảng biến thiên

Ta suy ra

Câu 3

Giá trị nhỏ nhất của hàm số y = $x^{3} - 3 x + 1$ trên đoạn [0;2] là:

A. $\underset{[0; 2]}{m i n y}$ = -3

B. $\underset{[0; 2]}{m i n y}$ = -2

C. $\underset{[0; 2]}{m i n y}$ = 1

D. $\underset{[0; 2]}{m i n y}$ = -1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = $|\frac{1}{4} x^{4} - \frac{19}{2} x^{2} + 30 x + m - 20|$ trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng

A. 210

B. -195

C. 105

D. 300

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số y = $\frac{a x + b}{c x + d}$ ( $c \neq 0$ và ad - bc $\neq$ 0) có đồ thị như hình vẽ.

Tìm khẳng định đúng trong các khẳng định sau:

A. ad < 0, ab > 0

B. bd > 0, ad < 0

C. ad > 0, ab < 0

D. ab < 0, ad < 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Hình vẽ bên là đồ thị của hàm số y = $a x^{4} + b x^{2} + c$ . Giá trị của biểu thức M = $a^{2} + b^{2} + c^{2}$ có thể nhận giá trị nào trong các giá trị sau

A. M = 18

B. M = 6

C. M = 20

D. M = 24

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Cho hàm số y = ${(x^{3} - 3 x + m)}^{2}$ . Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn [-1;1] bằng 1 là

Cho hàm số y = $a x^{3} + c x + d, a \neq 0$ có $\underset{x \in (- \infty; 0)}{m i n} f (x) = f (- 2)$ . Giá trị lớn nhất của hàm số y = f(x) trên đoạn [1;3] bằng

Giá trị nhỏ nhất của hàm số y = $x^{3} - 3 x + 1$ trên đoạn [0;2] là:

Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số y = $|\frac{1}{4} x^{4} - \frac{19}{2} x^{2} + 30 x + m - 20|$ trên đoạn [0;2] không vượt quá 20. Tổng các phần tử của S bằng

Cho hàm số y = $\frac{a x + b}{c x + d}$ ( $c \neq 0$ và ad - bc $\neq$ 0) có đồ thị như hình vẽ.

Tìm khẳng định đúng trong các khẳng định sau:

Hình vẽ bên là đồ thị của hàm số y = $a x^{4} + b x^{2} + c$ . Giá trị của biểu thức M = $a^{2} + b^{2} + c^{2}$ có thể nhận giá trị nào trong các giá trị sau