7 câu Trắc nghiệm Đường vuông góc và đường xiên có đáp án (Thông hiểu)

Hướng dẫn giải

Đáp án đúng là: D

Ta có: BC là cạnh đối diện của \(\widehat {\rm{A}}\)             (1)

           AC là cạnh đối diện của \(\widehat {\rm{B}}\)          (2)

Vì 80° > 60° nên \(\widehat {\rm{A}} > \widehat {\rm{B}}\)    (3)

Từ (1); (2) và (3) suy ra BC > AC (quan hệ giữa cạnh và góc trong tam giác).

Vậy ta chọn phương án D.

Hướng dẫn giải

Đáp án đúng là: A

Xét ∆DEF có: \(\widehat {\rm{D}} + \widehat {\rm{E}} + \widehat {\rm{F}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)

Hay \(38^\circ + 110^\circ + \widehat {\rm{F}} = 180^\circ \)

Suy ra \(\widehat {\rm{F}} = 180^\circ - 110^\circ - 38^\circ = 32^\circ \)

Vì \(32^\circ < 38^\circ < 110^\circ \) suy ra \(\widehat {\rm{F}} < \widehat {\rm{D}} < \widehat {\rm{E}}\) (1)

Ta lại có DE; EF; DF lần lượt là các cạnh đối diện của \(\widehat {\rm{F}};{\rm{ }}\widehat {\rm{D}};{\rm{ }}\widehat {\rm{E}}\)    (2)

Từ (1) và (2) suy ra DE < EF < DF (quan hệ giữa cạnh và góc trong một tam giác).

Do đó độ dài các cạnh của ∆DEF sắp xếp theo thứ tự tăng dần là: DE; EF; DF.

Vậy ta chọn phương án A.

Hướng dẫn giải

Đáp án đúng là: B

Ta có \(\widehat {\rm{A}};{\rm{ }}\widehat {\rm{B}};{\rm{ }}\widehat {\rm{C}}\) lần lượt là các góc đối diện của các cạnh BC; AC; AB.

Mà AB < BC < AC (do 5 cm < 9 cm < 13 cm).

Suy ra \(\widehat C < \widehat {\rm{A}} < \widehat B\) (quan hệ giữa cạnh và góc trong một tam giác).

Do đó các góc của ∆ABC sắp xếp theo thứ tự giảm dần là: \(\widehat {\rm{B}};{\rm{ }}\widehat {\rm{A}};{\rm{ }}\widehat {\rm{C}}\).

Vậy ta chọn phương án B.

Hướng dẫn giải

Đáp án đúng là: B

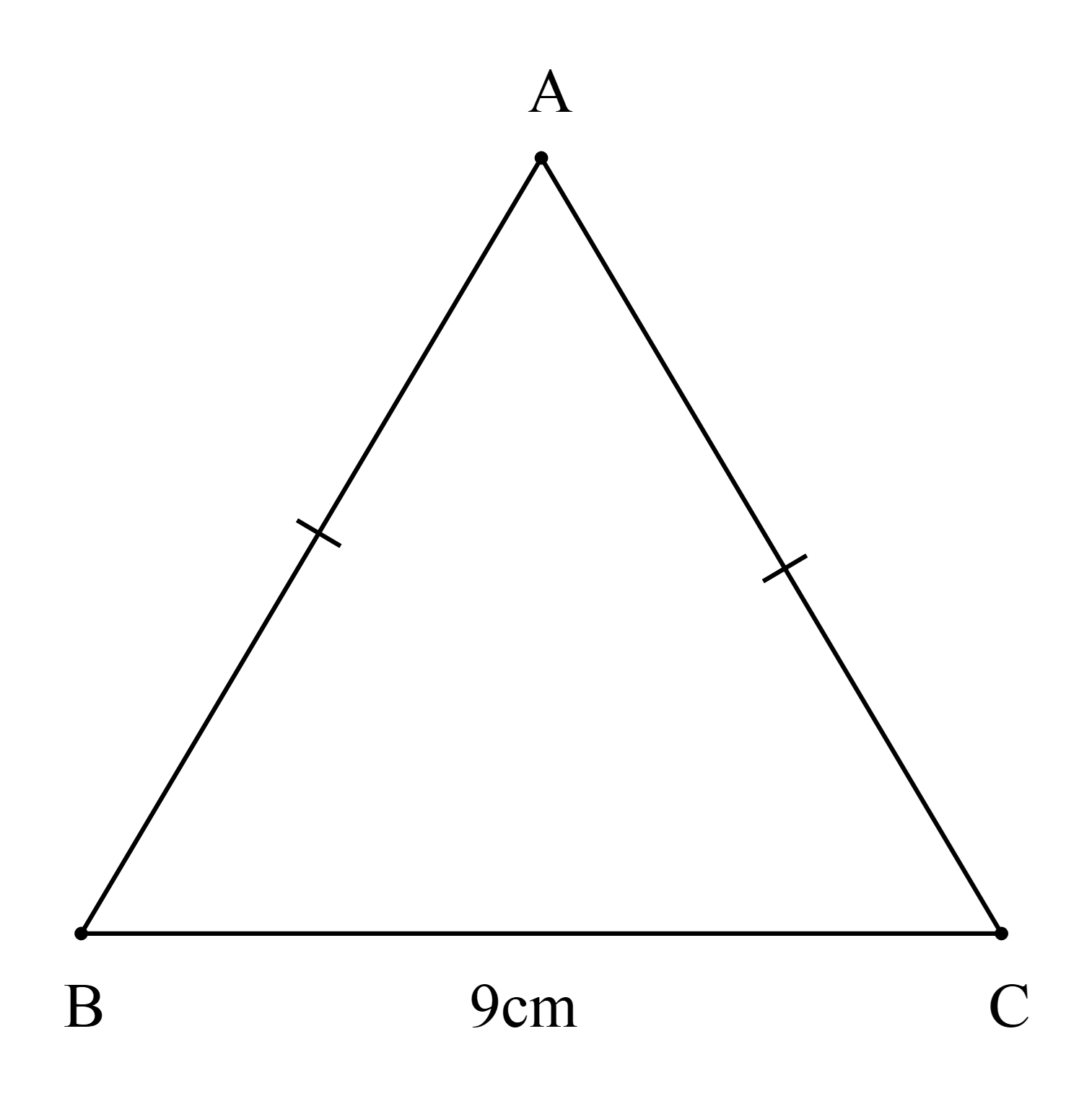
Do chu vi ∆ABC bằng 25 cm nên AB + AC + BC = 25 (cm).

Hay AB + AC + 9 = 25

Suy ra AB + AC = 25 – 9 = 16 (1)

Ta lại có AB = AC (do DABC cân tại A)    (2)

Từ (1) và (2) suy ra AB = AC = \(\frac{{16}}{2} = 8\) (cm).

Ta có AB; AC; BC lần lượt là cạnh đối diện của \(\widehat {\rm{C}}{\rm{; }}\widehat {\rm{B}}{\rm{; }}\widehat {\rm{A}}\).

Mà DABC cân tại A suy ra \(\widehat {\rm{B}} = \widehat {\rm{C}}\), do đó C đúng.

AB < BC suy ra \(\widehat {\rm{C}} < \widehat {\rm{A}}\) (quan hệ giữa cạnh và góc trong tam giác), do đó D đúng, B sai

AC < BC suy ra \(\widehat {\rm{B}} < \widehat {\rm{A}}\)(quan hệ giữa cạnh và góc trong tam giác), do đó A đúng.

Vậy ta chọn phương án B.

Hướng dẫn giải

Đáp án đúng là: A

Vì OB là đường vuông góc kẻ từ điểm O đến đường thẳng a;

     OA, OC là các đường xiên kẻ từ O đến đường thẳng a.

Nên OB < OA; OB < OC (1)

Xét ∆OAC có \(\widehat {\rm{A}} > \widehat {\rm{C}}\) (vì 65° > 30°)

Suy ra: OC > OA (quan hệ giữa góc và cạnh đối diện trong tam giác) (2)

Từ (1) và (2) suy ra: OB < OA < OC.

Vậy ta chọn phương án A.