3 câu Trắc nghiệm Đường vuông góc và đường xiên có đáp án (Vận dụng)

Hướng dẫn giải

Đáp án đúng là: C

Ta có MN : NP = 2 : 3 nên \(\frac{{MN}}{2} = \frac{{NP}}{3}\) suy ra \(\frac{{MN}}{8} = \frac{{NP}}{{12}}\).

Ta có NP : MP = 4 : 5 nên \(\frac{{NP}}{4} = \frac{{MP}}{5}\) suy ra \(\frac{{NP}}{{12}} = \frac{{MP}}{{15}}\).

Do đó \(\frac{{MN}}{8} = \frac{{NP}}{{12}} = \frac{{MP}}{{15}}\).

Lại có chu vi tam giác MNP bằng 70 cm nên MN + NP + MP = 70.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{{MN}}{8} = \frac{{NP}}{{12}} = \frac{{MP}}{{15}} = \frac{{MN + NP + MP}}{{8 + 12 + 15}} = \frac{{70}}{{35}} = 2\).

Suy ra:

• \(\frac{{MN}}{8} = 2\) nên MN = 2 . 8 = 16 (cm);

• \(\frac{{NP}}{{12}} = 2\) nên NP = 2 . 12 = 24 (cm);

• \(\frac{{MP}}{{15}} = 2\) nên MP = 2 . 15 = 30 (cm).

Trong tam giác MNP có MN < NP < MP nên \(\widehat P < \widehat M < \widehat N\) (Theo quan hệ giữa góc và cạnh đối diện trong tam giác).

Vậy góc P là góc nhỏ nhất.

Hướng dẫn giải

Đáp án đúng là: C

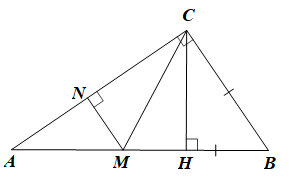
Xét DBCM có BM = BC nên DBCM cân tại B.

Suy ra \(\widehat {BCM} = \widehat {BMC}\).

Lại có \[\widehat {BCM} + \widehat {MCN} = 90^\circ \] và \(\widehat {BMC} + \widehat {MCH} = 90^\circ \)

Suy ra \[\widehat {MCN} = \widehat {MCH}\].

Xét DCMN và DCMH có:

\(\widehat {CNM} = \widehat {CHM} = 90^\circ \),

CM là cạnh chung,

\[\widehat {MCN} = \widehat {MCH}\] (chứng minh trên).

Do đó DCMN = DCMH (cạnh huyền – góc nhọn).

Suy ra CN = CH (hai cạnh tương ứng).

Ta có: AB + CH = AM + MB + CH.

Mà BM = BC (giả thiết) và CH = CN (chứng minh trên),

Do đó AB + CH = AM + BC + CN.

Mặt khác MN ⊥ AC tại N nên ∆ANM vuông tại N.

Do đó cạnh huyền AM là cạnh lớn nhất hay AM > AN.

Suy ra AB + CH = AM + BC + CN > AN + BC + CN

Hay AB + CH > AN + CN + BC = AC + BC.

Vậy AC + BC < AB + CH.

Ta chọn phương án C.

Hướng dẫn giải

Đáp án đúng là: A

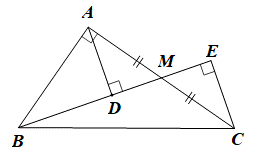
Do AD và CE vuông góc với BM nên \(\widehat {{\rm{ADM}}} = 90^\circ \) và \(\widehat {{\rm{CEM}}} = 90^\circ \).

Xét DADM và DCEM có:

\(\widehat {ADM} = \widehat {CEM}\left( { = 90^\circ } \right),\)

AM = CM (vì M là trung điểm của AC),

\(\widehat {{\rm{AMD}}} = \widehat {{\rm{CME}}}\) (hai góc đối đỉnh).

Suy ra ∆ADM = ∆CEM (cạnh huyền – góc nhọn).

Do đó DM = EM (hai cạnh tương ứng).

Ta có BD + BE = BD + (BM + ME) = (BD + ME) + BM

Mà DM = ME (chứng minh trên)

Nên BD + BE = (BD + DM) + BM = BM + BM = 2BM (1)

Vì BA, BM lần lượt là đường vuông góc và đường xiên kẻ từ B đến AC nên BM > AB.

Hay 2BM > 2AB (2)

Từ (1) và (2) suy ra BD + BE = 2BM > 2AB.

Do đó BD + BE > 2AB

Vậy ta chọn phương án A.