Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 7)

a) Ta có \({x^3} - 1 = \left( {x - 1} \right)\left( {{x^2} + x + 1} \right).\)

\[{x^2} + x + 1 = {\left( {x + \frac{1}{2}} \right)^2} + \frac{3}{4} > 0.\]

Điều kiện: \[\left\{ \begin{array}{l}{x^3} - 1 \ne 0\\x - 1 \ne 0\end{array} \right.\] nên \[\left\{ \begin{array}{l}\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) \ne 0\\x - 1 \ne 0\end{array} \right.\], do đó \[x \ne 1\].

Vậy điều kiện xác định của biểu thức \(P\) là \[x \ne 1\].

b) Với \(x \ne 1\), ta có

\(P = \frac{{6{x^2} + 8x + 7}}{{{x^3} - 1}} + \frac{x}{{{x^2} + x + 1}} - \frac{6}{{x - 1}}\)

\( = \frac{{6{x^2} + 8x + 7}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} + \frac{{x\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} - \frac{{6\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)

\( = \frac{{6{x^2} + 8x + 7 + {x^2} - x - 6{x^2} - 6x - 6}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)

\( = \frac{{{x^2} + x + 1}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{1}{{x - 1}}.\)

Vậy với \(x \ne 1\) thì \(P = \frac{1}{{x - 1}}.\)

c) Thay \(x = \frac{1}{2}\) vào biểu thức \(P\), ta được:

\(P = \frac{1}{{x - 1}} = \frac{1}{{\frac{1}{2} - 1}} = \frac{1}{{ - \frac{1}{2}}} = - 2.\)

Vậy với \(x = \frac{1}{2}\) thì \(P = - 2.\)

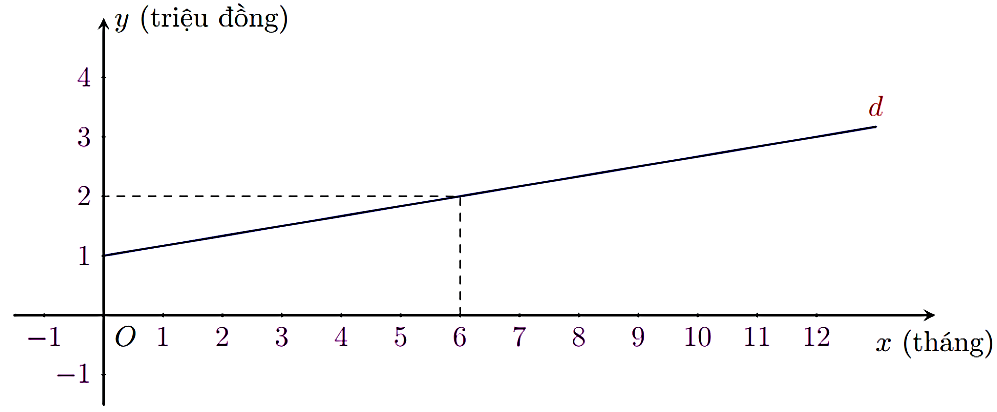
a) Gọi hàm số bậc nhất cần tìm là \(y = ax + b\,\,\left( {a \ne 0} \right).\)

Theo giả thiết, ta có

• Với \(x = 0\,;\,\,y = 1\) thì \(0a + b = 1\) hay \(b = 1\).

• Với \(x = 6\,;\,\,y = 2\) thì \(6a + 1 = 2\) hay \(a = \frac{1}{6}\).

Vậy \(\left( d \right):y = \frac{1}{6}x + 1\).

b) Giao điểm của đường thẳng \(d\) với trục tung có ý nghĩa là chi phí ban đầu người dùng trả cho nhà mạng là 1 triệu đồng.

Trong thời gian 12 tháng, người dùng phải trả số tiền là: \(\frac{1}{6} \cdot 12 + 1 = 3\) (triệu đồng).

Nửa chu vi của hình chữ nhật là: \[132:2 = 66\]\[\left( m \right)\].

Gọi \[x\]\[\left( m \right)\] là chiều dài của hình chữ nhật \[\left( {0 < x < 66} \right)\]

Chiều rộng của hình chữ nhật là \[66 - x\] \[\left( m \right)\].

Diện tích của hình chữ nhật là \[x\left( {66 - x} \right)\] \[\left( {{m^2}} \right)\]

Chiều dài của hình chữ nhật sau khi tăng là \[x + 8\] \[\left( m \right)\].

Chiều rộng của hình chữ nhật sau khi giảm là: \[66 - x - 4 = 62 - x\] \[\left( m \right)\].

Diện tích của hình chữ nhật lúc sau là: \[\left( {x + 8} \right)\left( {62 - x} \right)\]\[\left( {{m^2}} \right)\]

Theo đề bài, ta có phương trình:

\[\left( {x + 8} \right)\left( {62 - x} \right) = x\left( {66 - x} \right) + 52\]

\[ - {x^2} + 54x + 496 = - {x^2} + 66x + 52\]

\[66x - 54x = 496 - 52\]

\[12x = 444\]

\(x = 37\) (TMĐK)  

Chiều rộng của hình chữ nhật là \[66 - 37 = 29\] \[\left( m \right)\].

Vậy chiều dài và chiều rộng của hình chữ nhật lần lượt là \[37\,\,m\] và \[29\,\,m\].