10 Bài tập Xác định và tính góc giữa hai đường thẳng (có lời giải)
27 người thi tuần này 4.6 773 lượt thi 10 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
Bài tập Giới hạn cơ bản, nâng cao có lời giải (P1)
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 1
20 câu trắc nghiệm Toán 11 Kết nối tri thức Mẫu số liệu ghép nhóm có đáp án
20 câu Trắc nghiệm Toán 11 Cánh diều Bài 5. Hình lăng trụ và hình hộp (Đúng-sai, trả lời ngắn) có đáp án
20 câu Trắc nghiệm Toán 11 Cánh diều Bài 4. Hai mặt phẳng song song (Đúng-sai, trả lời ngắn) có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: D
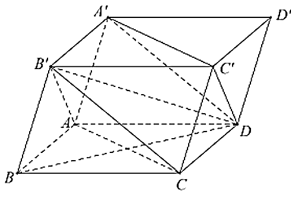
Ta có: AC // A'C' (do ABCD.A'B'C'D') là hình hộp.
Do đó, (AC, A'D) = (A'C', A'D) = (do giả thiết tam giác DA'C' nhọn).
Lời giải
Đáp án đúng là: D
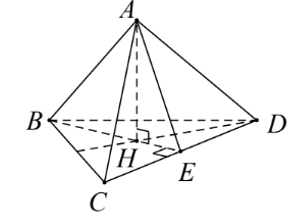
Gọi H là tâm đường tròn ngoại tiếp tam giác BCD
Do đó, AH vuông góc với (BCD).
ABCD là tứ diện đều tất cả các cạnh bằng nhau nên tam giác BCD đều.
Gọi E là trung điểm của CD ⇒ BE vuông góc với CD.
Do AH vuông góc với (BCD) nên AH vuông góc với CD.
Ta có: .Lời giải
Đáp án đúng là: A
Không mất tính tổng quát, giả sử tứ diện ABCD có cạnh bằng a.
Gọi H là tâm đường tròn ngoại tiếp tam giác BCD nên AH vuông góc với (BCD).
Gọi E là trung điểm AC, ta có:
ME // AB ⇒ (AB, DM) = (ME, MD)
Ta có: cos(AB, DM) = cos(ME, MD)
Do các mặt của tứ diện đều là tam giác đều, từ đó ta dễ dàng tính được độ dài các cạnh của tam giác MED: ME = ; ED = MD = .
Xét tam giác MED, ta có:
.
Từ đó .
Lời giải
Đáp án đúng là: D
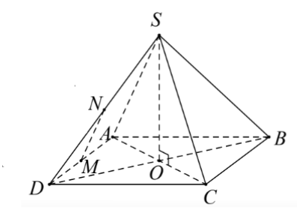
Gọi O là tâm của hình vuông ABCD, do đó, O là tâm đường tròn ngoại tiếp của hình vuông ABCD (1)
Ta có: SA = SB = SC = SD nên S nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).
Từ (1) và (2) ta có: SO vuông góc với (ABCD).
Từ giả thiết ta có: MN song song với SA (do MN là đường trung bình của tam giác SAD)
⇒ (MN, SC) = (SA, SC)
Xét tam giác SAC có:
SA2 + SC2 = a2 + a2 = 2a2
AC2 = AD2 + DC2 = 2a2
Suy ra SA2 + SC2 = AC2.
Do đó, tam giác SAC vuông tại S nên SA vuông góc với SC.
Vậy (MN, SC) = (SA, SC) = 90°.
Lời giải
Đáp án đúng là: C
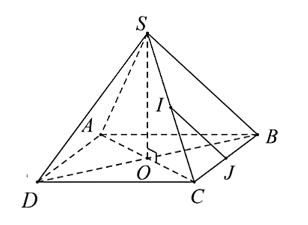
Gọi O là tâm của hình vuông ABCD
Do đó, O là tâm của đường tròn ngoại tiếp của hình vuông ABCD (1)
Ta có: SA = SB = SC = SD nên S nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2)
Từ (1) và (2) ⇒ SO vuông góc với (ABCD)
Ta lại có: IJ // SB (do IJ là đường trung bình của tam giác SAB)
⇒ (IJ, CD) = (SB, AB)
Mặt khác, ta lại có tam giác SAB đều, do đó ⇒ (IJ, CD) = (SB, AB) = .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 30
B. 45
C. 60
D. 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.