7 câu Trắc nghiệm Tính chất ba đường trung trực của tam giác có đáp án (Thông hiểu)

Hướng dẫn giải

Đáp án đúng là: A

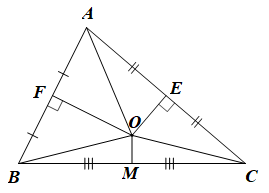
Do các đường trung trực của AB và AC cắt nhau tại O nên O là giao điểm của ba đường trung trực của tam giác ABC.

Do đó O nằm trên đường trung trực của BC.

Mà M là trung điểm của BC nên OM là trung trực của BC.

Suy ra OM vuông góc với BC nên \(\widehat {OMC} = 90^\circ \).

Vậy ta chọn phương án A.

Hướng dẫn giải

Đáp án đúng là: C

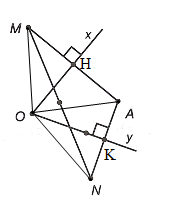
Xét tam giác AMN có O là giao điểm hai đường trung trực của AM và AN nên O cách đều ba đỉnh A, M, N hay OA = OM = ON.

Gọi H là giao điểm của Ox và MA, K là giao điểm của Oy và AN.

Xét ΔAOH và ΔMOH có

\(\widehat {OHA} = \widehat {OHM} = 90^\circ \),

OA = OM (chứng minh trên),

OH là cạnh chung

Do đó ΔAOH = ΔMOH (cạnh huyền – cạnh góc vuông).

Suy ra \(\widehat {AOH} = \widehat {MOH}\)(hai góc tương ứng)

Chứng minh tương tự ta cũng có:

ΔAOK = ΔNOK (cạnh huyền – cạnh góc vuông).

Suy ra \(\widehat {AOK} = \widehat {NOK}\)(hai góc tương ứng)

Ta có \(\widehat {MON} = \widehat {MOH} + \widehat {AOH} + \widehat {AOK} + \widehat {KON}\)

Mà \(\widehat {AOH} = \widehat {MOH}\), \(\widehat {AOK} = \widehat {NOK}\) (chứng minh trên).

Suy ra \(\widehat {MON} = 2\widehat {AOH} + 2\widehat {AOK}\)

Hay \(\widehat {MON} = 2(\widehat {AOH} + \widehat {AOK}) = 2\widehat {xOy} = 2.50^\circ = 100^\circ \).

Vậy ta chọn phương án C.

Hướng dẫn giải

Đáp án đúng là: C

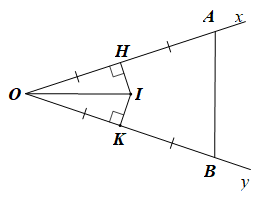
Vì HI là trung trực của OA nên IH ⊥ OA, OH = HA = \(\frac{1}{2}\)OA;

Vì KI là trung trực của OB nên IK ⊥ OB, OK = KB = \(\frac{1}{2}\)OB.

Mà OA = OB (giả thiết) nên OH = OK.

Xét DOIH và DOIK có

\(\widehat {OHI} = \widehat {OKI}( = 90^\circ )\),

OI là cạnh chung,

OH = OK (chứng minh trên)

Do đó DOIH = DOIK (cạnh huyển – cạnh góc vuông).

Suy ra \(\widehat {HOI} = \widehat {KOI}\) (hai góc tương ứng).

Do đó OI là tia phân giác của \(\widehat {xOy}\), nên (I) đúng.

Xét DOAB có IH là trung trực của OA, IK là trung trực của OB, IH cắt IK tại H nên I là giao điểm của ba đường trung trực trong tam giác OAB.

Do đó OI là trung trực của AB, nên (II) đúng.

Vậy ta chọn phương án C.

Hướng dẫn giải

Đáp án đúng là: B

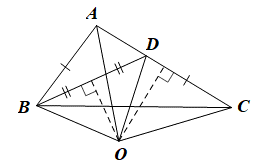
Vì O thuộc đường trung trực của AC nên OA = OC;

Vì O thuộc đường trung trực của BD nên OB = OD.

Xét ΔAOB và ΔCOD có

OA = OC (chứng minh trên),

OB = OD (chứng minh trên),

AB = CD (giả thiết)

Do đó ΔAOB = ΔCOD (c.c.c).

Vậy ta chọn phương án B.

Hướng dẫn giải

Đáp án đúng là: B

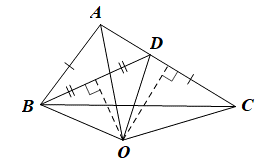
Vì O thuộc đường trung trực của AC nên OA = OC;

Vì O thuộc đường trung trực của BD nên OB = OD.

Xét ΔAOB và ΔCOD có

OA = OC (chứng minh trên),

OB = OD (chứng minh trên),

AB = CD (giả thiết)

Do đó ΔAOB = ΔCOD (c.c.c).

Suy ra \(\widehat {OAB} = \widehat {OCD}\) (hai góc tương ứng)   (1)

Mặt khác OA = OC nên tam giác OAC cân tại O

Suy ra \(\widehat {OAC} = \widehat {OCA}\) hay \(\widehat {OAC} = \widehat {OCD}\)      (2)

Từ (1) và (2) ta có \(\widehat {OAB} = \widehat {OAC}\) nên AO là tia phân giác của góc BAC.

Vậy ta chọn phương án B.