12 bài tập Tính bán kính đường tròn có lời giải
31 người thi tuần này 4.6 168 lượt thi 12 câu hỏi 45 phút
🔥 Đề thi HOT:
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: B
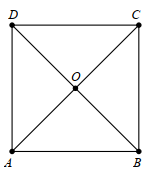
Gọi O là giao hai đường chéo của hình vuông ABCD. Khi đó theo tính chất của hình vuông, ta có: OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = \(\frac{{AC}}{2}\).
Xét tam giác ABC vuông cân tại B, ta có:
AC = \(\sqrt {A{B^2} + B{C^2}} = 3\sqrt 2 \)
Suy ra OA = \(\frac{{AC}}{2} = \frac{{3\sqrt 2 }}{2}\).
Vậy bán kính của đường tròn là R = OA = \(\frac{{3\sqrt 2 }}{2}\) cm.
Lời giải
Đáp án đúng là: B

Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền BC, ban kính R = \(\frac{{BC}}{2}\).
Theo định lí Pythagore ta có: BC = \(\sqrt {A{C^2} + A{B^2}} = 25\) nên bán kính R = \(\frac{{25}}{2}\).
Lời giải
Đáp án đúng là: C

Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền BC, ban kính R = \(\frac{{BC}}{2}\).
Theo định lí Pythagore ta có: BC = \(\sqrt {A{C^2} + A{B^2}} = 13\) nên bán kính R = \(\frac{{13}}{2}\).
Lời giải
Đáp án đúng là: D
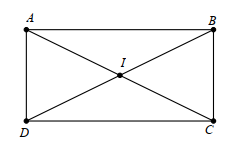
Gọi I là giao điểm của hai đường chéo, ta có: IA = IB = IC = ID (vì BD = AC và I là trung điểm của mỗi đường).
Nên bốn điểm A, B, C, D cùng thuộc đường tròn tâm I bán kính R = \(\frac{{AC}}{2}\).
Theo định lí Pythagore trong tam giác ABC ta có:
AC = \(\sqrt {B{C^2} + A{B^2}} = 13\) cm.
Do đó, R = \(\frac{{AC}}{2}\) = 6,5 cm.
Vậy bán kính cần tìm là R = 6,5 cm.
Lời giải
Đáp án đúng là: A
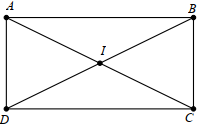
Gọi I là giao điểm của hai đường chéo, ta có: IA = IB = IC = ID (vì DB = AC và I là trung điểm mỗi đường)
Nên bốn điểm A, B, C, D cùng thuộc đường tròn tâm I bán kính R = \(\frac{{AC}}{2}\).
Theo định lí Pythagore trong tam giác vuông ABC, ta có:
AC = \(\sqrt {B{C^2} + A{B^2}} = \sqrt {{6^2} + {8^2}} = 10\) nên R = \(\frac{{AC}}{2}\) = 5 cm.
Vậy bán kính cần tìm là R = 5 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
34 Đánh giá
50%
40%
0%
0%
0%