Đề cương ôn tập Giữa kì 2 Toán 7 Cánh diều cấu trúc mới (Tự luận) có đáp án - Phần 2

Hướng dẫn giải

\(AF = EC\) (cmt); \[\widehat {DAF} = \widehat {DEC} = 90^\circ \]; \(AD = DE\) (vì \(\Delta ABD = \Delta EBD\));

Do đó \[\Delta ADF = \Delta EDC\,\,{\rm{(c}}{\rm{.g}}{\rm{.c)}}\].

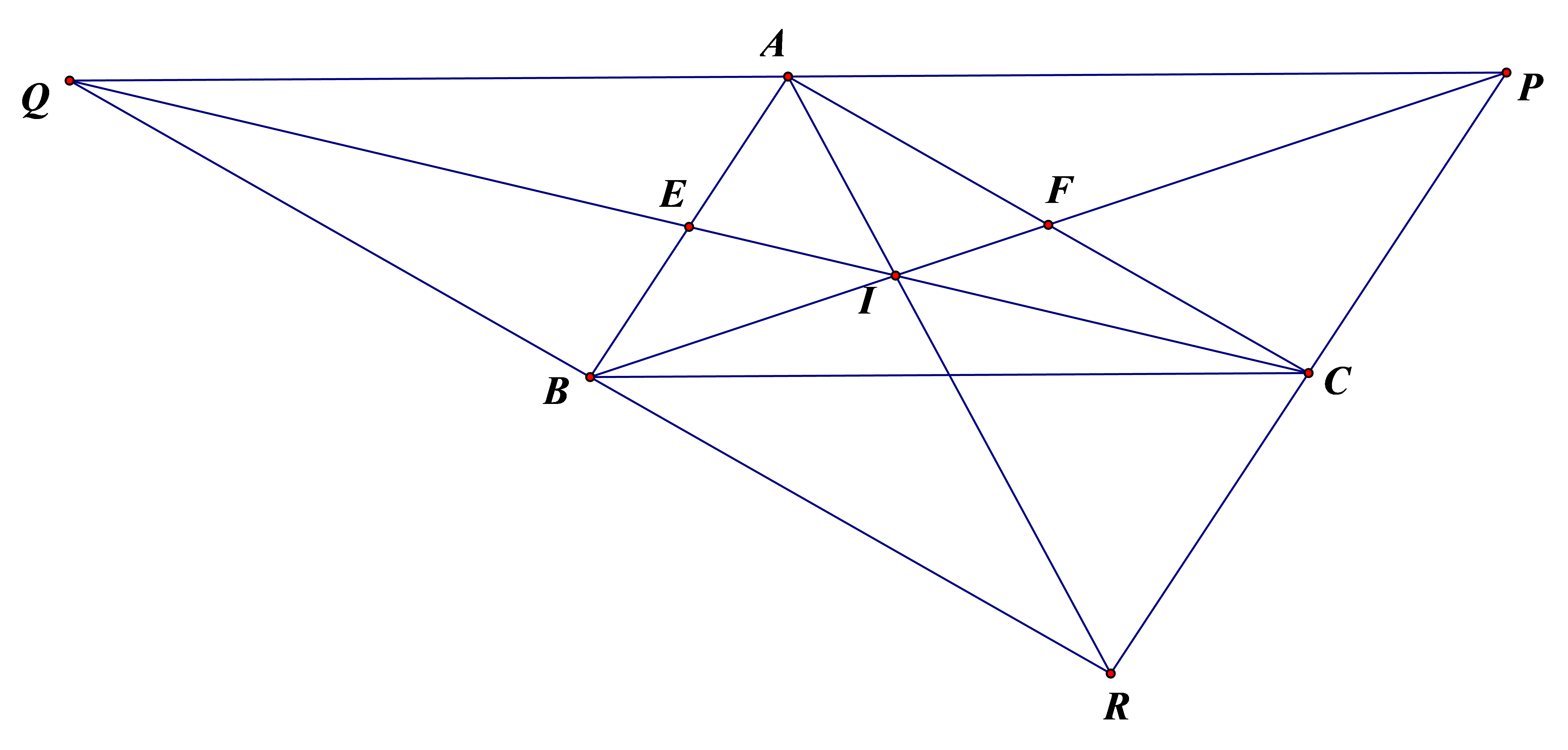
a) • Xét \(\Delta AQE\) và \(\Delta BCE\) có:

\(AE = BE\) (vì \(E\) là trung điểm của \(AB\))

\[\widehat {AEQ} = \widehat {BEP}\] (hai góc đối đỉnh)

\(QE = CE\) (gt)

Do đó \(\Delta AQE = \Delta BCE\,\,{\rm{(c}}{\rm{.g}}{\rm{.c)}}\).

Suy ra \[AQ = BC\] (hai cạnh tương ứng)     (1)

• Xét \(\Delta APF\) và \(\Delta CBF\) có

\(PF = BF\) (gt)

\[\widehat {AFP} = \widehat {BFC}\] (hai góc đối đỉnh)

\(AE = BE\) (vì \(F\) là trung điểm của \(AC\))

Do đó \[\Delta APF = \Delta CBF\,\,{\rm{(c}}{\rm{.g}}{\rm{.c)}}\].

Suy ra \[AP = BC\] (hai cạnh tương ứng)                (2)

Từ (1) và (2) suy ra \[AP = AQ\].

b) Ta có \(\widehat {QAB} = \widehat {ABC}\,;\,\,\widehat {PAC} = \widehat {ACB}\) (các cặp góc tương ứng của tam giác bằng nhau)

Xét tam giác \(ABC\) có \[\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = 180^\circ \] (tổng ba góc trong một tam giác)

Suy ra \[\widehat {QAB} + \widehat {BAC} + \widehat {PAC} = \widehat {ABC} + \widehat {BAC} + \widehat {ACB} = 180^\circ \].

Do đó, ba điểm \(P,\,\,A\,,\,\,Q\) thẳng hàng.

c) Ta có \(\widehat {QAB} = \widehat {ABC}\,;\,\,\widehat {PAC} = \widehat {ACB}\) (cmt)

Suy ra \(BQ\,{\rm{//}}\,AC\) và \(CP\,{\rm{//}}\,AB\) (các cặp góc so le trong).

d) Ba đường thẳng \(AR\,,\,\,BP\,,\,\,CQ\) là ba đường trung tuyến của tam giác \[QRP\] nên đồng quy.

a) Xét \[\Delta AMB\] và \[\Delta CMD\] có:

\[MD = MB\] (giả thiết)

\[\widehat {AMB} = \widehat {CMD}\] (2 góc đối đỉnh)

\[MA = MC\] (giả thiết)

Suy ra \[\Delta AMB = \Delta CMD\] (c.g.c)

b) Xét \[\Delta AMD\] và \[\Delta CMB\] có: \[MD = MB\] (giả thiết), \[\widehat {AMD} = \widehat {CMB}\] (đối đỉnh), \[MA = MC\] (giả thiết)

Vậy \[\Delta AMD = \Delta CMB\] (c.g.c) suy ra \[\widehat {ADM} = \widehat {CBM}\] (hai góc tương ứng), mà hai góc này lại ở vị trí sole trong nên \[AD\,{\rm{//}}\,BC\] (dấu hiệu nhận biết)

c) Ta có: \[\Delta AMB = \Delta CMD\] (chứng minh trên) suy ra \[\widehat {MAB} = \widehat {MCD}\] (hai góc tương ứng) mà hai góc này lại ở vị trí sole trong nên \[AB\,{\rm{//}}\,\,CD\] (1)

Ta lại có: \[MH \bot AB\] (giả thiết) (2). Từ (1) và (2) suy ra \[MH \bot CD\] và \[MK \bot DC\] (giả thiết) suy ra 3 điểm \[H,M,K\] thẳng hàng (định lý)

Xét \[\Delta AMH\] và \[\Delta CMK\] có:

\[\widehat {AHM} = \widehat {MKC} = 90^\circ \] (giả thiết)

\[AM = MC\] (giả thiết)

\[\widehat {AMH} = \widehat {CMK}\] (đối đỉnh)

Vậy \[\Delta AMH = \Delta CMK\] (ch – gn) suy ra \[AM = MC\] hay \[M\] là trung điểm \[HK\].

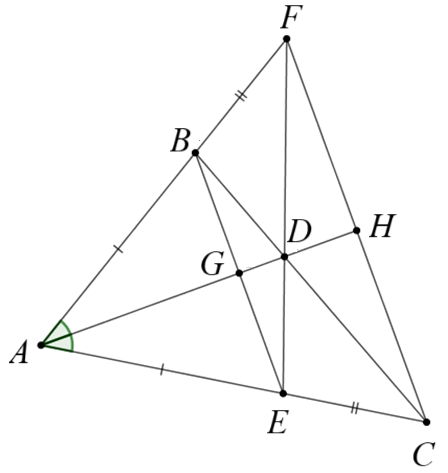
a) Chứng minh \(\Delta BDF = \Delta EDC\).

Vì \(AD\) là phân giác \(\widehat {BAC}\) nên \(\widehat {BAD} = \widehat {CAD}\).

Xét \(\Delta ADF\) và \(\Delta ADC\) có:

\(AF = AC\,;\,\,\widehat {FAD} = \widehat {CAD}\,;\,\,AD\) chung.

Do đó \(\Delta ADF = \Delta ADC\) (c.g.c)

Suy ra \(\widehat {AFD} = \widehat {ACD}\) (hai góc tương ứng) và \(FD = CD\) (hai cạnh tương ứng)

Vì \(AF = AC\,;\,\,AB = AE\) suy ra \(BF = EC\)

Xét tam giác \(BDF\) và tam giác \(EDC\) có:

\(BF = EC\,;\,\,\,\widehat {BFD} = \widehat {ECD}\,;\,\,\,FD = CD\).

Do đó \(\Delta BDF = \Delta EDC\) (c.g.c)

b) Theo câu a) \(\Delta BDF = \Delta EDC\) suy ra \(\widehat {BDF} = \widehat {ECD}\).

Mà \(\widehat {BDE} + \widehat {EDC} = 180^\circ \) (hai góc kề bù) nên\(\widehat {BDE} + \widehat {FDB} = 180^\circ \), do đó \(\widehat {FDE} = 180^\circ \).

Suy ra ba điểm \(F,\,D,\,E\) thẳng hàng.

c) Gọi \(G,\,H\) theo thứ tự là giao điểm của \(AD\) và \(BE,\,CF\).

Xét tam giác \(ABG\) và \(AEG\) có:

\(AB = AE\,;\,\,\widehat {BAG} = \widehat {EAG}\,;\,\,AG\) chung.

Suy ra \(\Delta ABG = \Delta AEG\) (c.g.c)

Do đó, \(\widehat {AGB} = \widehat {AGE}\) (hai góc tương ứng) và \(GB = GE\) (hai cạnh tương ứng) (1)

Mà \(\widehat {AGB} + \widehat {AGE} = 180^\circ \) suy ra \(\widehat {AGB} = \widehat {AGE} = 90^\circ \) (2)

Từ (1) và (2) suy ra \(AD\) là đường trung trực \(BE\).

Chứng minh tương tự ta có \(AD\) là đường trung trực \(CF\).

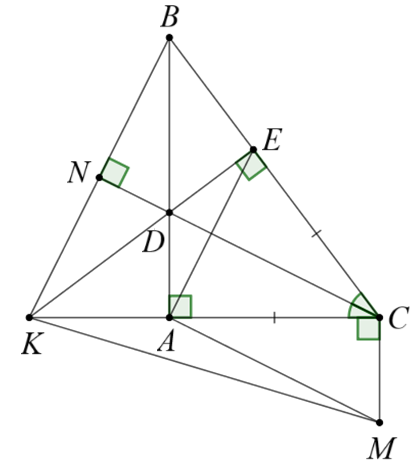
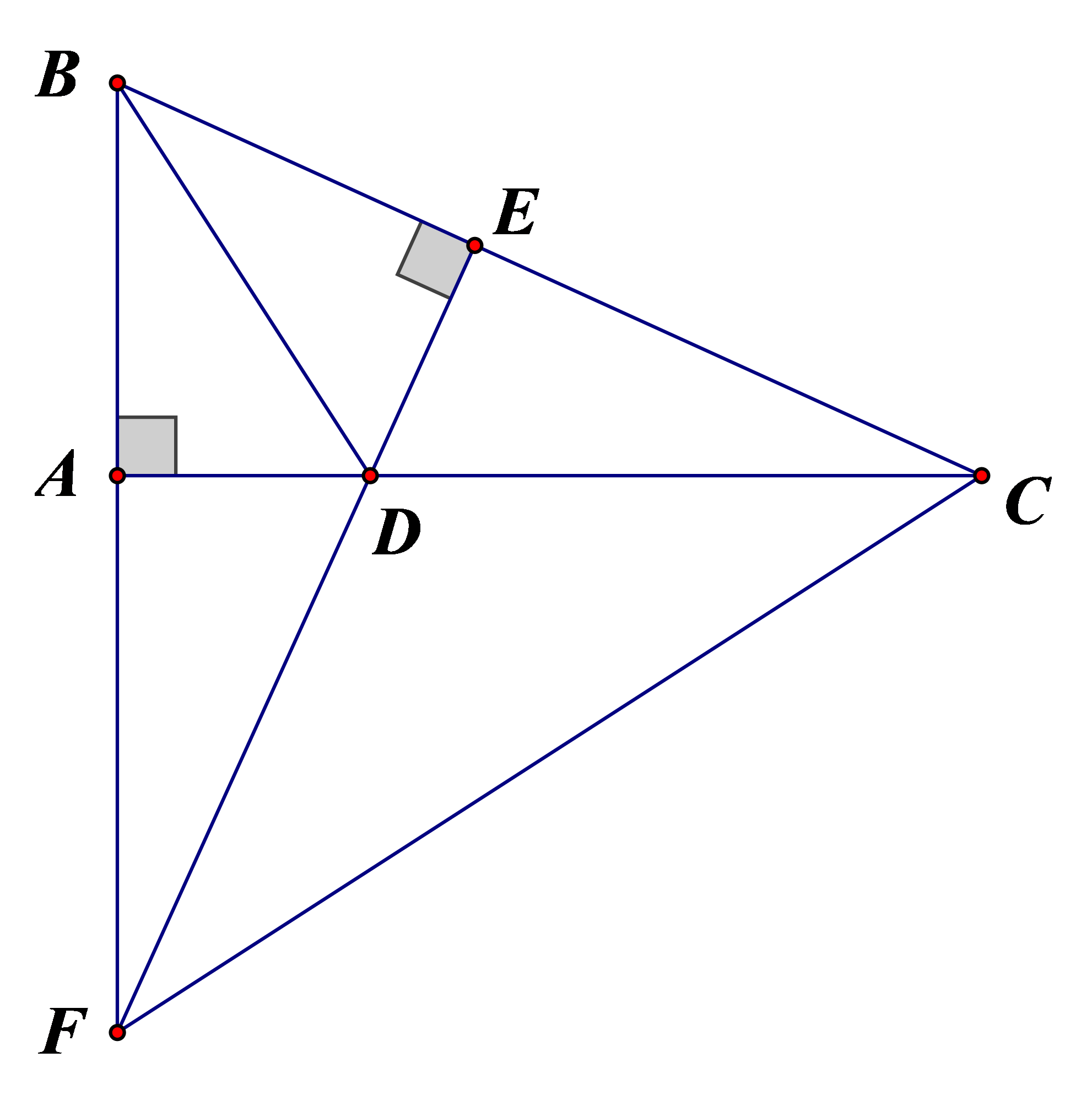
a) Vì \(CD\) là phân giác \(\widehat {BCA}\) suy ra \(\widehat {BCD} = \widehat {ACD}\).

Xét \(\Delta ACD\) và \(\Delta ECD\) có:

\(AC = AF\,;\,\,\widehat {BCD} = \widehat {ACD}\,;\,\,CD\) chung.

Do đó \(\Delta ACD = \Delta ECD\) (c.g.c).

Suy ra \(\widehat {CED} = \widehat {CAD} = 90^\circ \) (hai góc tương ứng)

Suy ra \(DE \bot BC\).

b) Vì \(AM\parallel CD\) suy ra \(\widehat {MAC} = \widehat {DCA}\) (hai góc so le trong)

Vì \(CM \bot CA\) nên \(\widehat {MCA} = 90^\circ \).

Xét \(\Delta CAD\) và \(\Delta ACM\) có:

\(\widehat {DAC} = \widehat {MCA} = 90^\circ \,;\,\,CA\) chung; \(\widehat {DCA} = \widehat {MAC}\).

Do đó \(\Delta CAD = \Delta ACM\) (g.c.g).

Suy ra (hai cạnh tương ứng).

c) Xét tam giác \(NBC\) và tam giác \(NKC\) có:

\(\widehat {BNC} = \widehat {KNC} = 90^\circ \,;\,\,NC\) chung; \(\widehat {BCN} = \widehat {CKN}\)

Suy ra \(\Delta NBC = \Delta NKC\,\)(g.c.g)

Do đó \(\widehat {NBC} = \widehat {NKC}\,;\,\,NB = NK\).

Xét tam giác \(NBD\) và tam giác \(NKD\) có:

\(NB = ND\,;\,\,\widehat {BND} = \widehat {KND}\,;\,\,ND\) chung.

Suy ra \(\Delta NBD = \Delta NKD\) (c.g.c).

Do đó, \(\widehat {NBD} = \widehat {NKD}\) (hai góc tương ứng)

d) Xét tam giác \(BKE\) và tam giác \(BKC\) có:

\[\widehat {BKE} = \widehat {BKA}\,;\,\,BK\] chung; \[\widehat {BKE} = \widehat {KBA}\].

Do đó \(\Delta BKE = \Delta BKC\) (g.c.g)

Suy ra \(\widehat {BEK} = \widehat {KAB} = 90^\circ \) (hai góc tương ứng)

Suy ra \(KE \bot BC\).

Mà \(DE \bot AC\).

Suy ra ba điểm \(K,\,D,\,E\) thẳng hàng.

a) Xét \(\Delta AHC\) và \(\Delta KCH\) có

\(AH = HK\) (\(H\) là trung điểm của \(AK\))

\(\widehat {AHC} = \widehat {CHK}\) (\(AH \bot BC\))

\(CH\) là cạnh chung

Do đó \(\Delta AHC = \Delta KHC\) (cgc).

b) Vì \[\Delta AHC = \Delta KHC\] (chứng minh trên) do đó \[AC = CK\] (2 cạnh tương ứng)                            (1)

Xét \[\Delta AEC\] và \[\Delta DEB\] ta có :

\[AE = ED\] (\[E\] là trung điểm của \[AD\])

\[BE = CE\] (\[E\] là trung điểm của \[BE\]) \[\widehat {AEC} = \widehat {BEC}\] (đối đỉnh)

Do đó \[\Delta AEC = \Delta DEB\] (c.g.c), suy ra \[AC = DB\] (2 cạnh tương ứng)                  (2)

Từ (1) và (2) suy ra \[BD = AC = CK\].

c) Xét \[\Delta AHC\] và \[\Delta KHE\] ta có \[AH = KH\], \[\widehat {AHE} = \widehat {KHE}\], \[HE\] là cạnh chung

Suy ra \[\Delta AHC = \Delta KHE\] (c.g.c) do đó \[\widehat {AEH} = \widehat {KEH}\] (2 góc tương ứng)

Suy ra \[EH\] là tia phân giác \[AEK\].

Vì \[\Delta AHE = \Delta KHE\] nên \[AE = KE\] mà \[AE = ED\]

Suy ra \[KE = ED\] do đó \[\Delta KED\] cân tại \[E\] nên \[\widehat {EKD} = \widehat {EDK}\].

\[\widehat {EDK} + \widehat {KED} = 90^\circ \] nên \[\widehat {EKD} = \frac{{180^\circ - \widehat {KED}}}{2}\]

Lại có \[\widehat {AKE} + \widehat {KED} = 180^\circ \] suy ra \[\widehat {AKE} = 180^\circ - \widehat {KED}\].

\[\widehat {AEH} + \widehat {HEK} = 180^\circ - \widehat {KED}\]

\[\widehat {HEK} = 180^\circ - \widehat {KED}\]

\[\widehat {HEK} = \frac{{180^\circ - \widehat {KED}}}{2}\]                          (4)

Từ (3) và (4) suy ra \[\widehat {HEK} = \widehat {ABC}\] mà chúng là 2 góc so le trong

Do đó \[HE{\rm{//}}KD\] hay \[BC{\rm{//}}KD\].

d) Xét \[\Delta KEN\] và \[\Delta DEN\] \[CE = ED\] (\[EN\] chung) \[KN = ND\] (\[N\] là trung điểm của \[KD\])

Suy ra \[\Delta KEN = \Delta DEN\] (c.c.c) nên \[\widehat {ENK} = \widehat {END}\] mà \[\widehat {ENK} + \widehat {END} = 180^\circ \].

Suy ra \[\widehat {ENC} = \widehat {END} = \frac{{180^\circ }}{2} = 90^\circ \] hay \[EN \bot KD\].

\[\Delta KBE = \Delta DCE\] suy ra \[BK = CD\] (2 cạnh tương ứng)

\[\Delta BKD = \Delta CDK\] (c.c.c) do đó \[\widehat {BDK} = \widehat {CKD}\] (2 góc tương ứng)

Suy ra \[\Delta KID\] cân tại \[I\] nên \[IK = ID\] xét \[\Delta KIN = \Delta DIN\] do đó \[\widehat {INK} - \widehat {IND}\].

Mà \[\widehat {INK} + \widehat {IND} = 180^\circ \] suy ra \[\widehat {INK} = \widehat {IND} = 90^\circ \] hay \[IN \bot KD\].