12 bài tập Tính độ dài đoạn thẳng, góc liên quan đến tiếp tuyến của đường tròn có lời giải
33 người thi tuần này 4.6 164 lượt thi 12 câu hỏi 45 phút
🔥 Đề thi HOT:
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: B
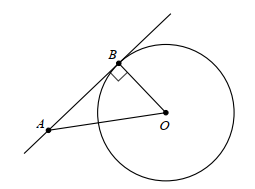
Vì AB là tiếp tuyến và B là tiếp điểm nên OB = R = 5 cm; AB ⊥ OB tại B.
Áp dụng định lí Pythagore vào tam giác ABO vuông tại B, ta được:
AB = \(\sqrt {O{A^2} - O{B^2}} = \sqrt {{{13}^2} - {5^2}} = 12\) cm.
Lời giải
Đáp án đúng là: B
Để AC là tiếp tuyến của đường tròn (B) thì AC ⊥ BA tại A.
Áp dụng định lí Pythagore vào tam giác ABC, ta có:
BC = \(\sqrt {C{A^2} + A{B^2}} = \sqrt {{6^2} + {8^2}} = 10\) cm.
Lời giải
Đáp án đúng là: D

Vì AB là tiếp tuyến và B là tiếp điểm nên OB = R = 6 cm; AB ⊥ OB tại B.
Áp dụng định lí Pythagore vào tam giác ABO vuông tại B, ta được:
AB = \(\sqrt {O{A^2} - O{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\) cm.
Lời giải
Đáp án đúng là: A
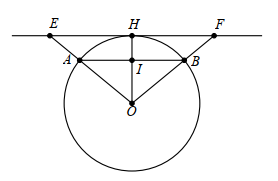
Kẻ OH ⊥ EF tại H và cắt AB tại I suy ra OI ⊥ AB (vì AB ∕∕ EF)
Xét (O) có OI ⊥ AB tại I nên I là trung điểm của AB.
Suy ra IA = IB = \(\frac{{AB}}{2} = 0,6R\). Lại có OA = R.
Áp dụng định lí Pythagore cho tam giác OAI ta có: OI = \(\sqrt {O{A^2} - I{A^2}} = 0,8R\).
Mà AI ∕∕ EH nên \(\frac{{AI}}{{EH}} = \frac{{OI}}{{OH}} = \frac{{0,8R}}{R}\) nên EH = \(\frac{{0,6R}}{{0,8}} = 0,75R\).
∆OEF cân tại O (vì \(\widehat E = \widehat F = \widehat {BAO} = \widehat {ABO}\)) có OH ⊥ EF nên H là trung điểm của EF.
Vì EF = 2EH = 1,5R nên diện tích tam giác EOF là \(\frac{1}{2}OH.EF = 0,75{R^2}\).
Lời giải
Đáp án đúng là: C
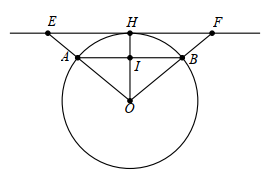
Kẻ OH ⊥ EF tại H và cắt AB tại I suy ra OI ⊥ AB (vì AB ∕∕ EF)
Xét (O) có OI ⊥ AB tại I nên I là trung điểm của AB.
Suy ra IA = IB = \(\frac{{AB}}{2}\) = 4,8 cm. Lại có OA = 6 cm.
Áp dụng định lí Pythagore cho tam giác OAI ta có: OI = \(\sqrt {O{A^2} - I{A^2}} \) = 3,6 cm.
Mà AI ∕∕ EH nên \(\frac{{AI}}{{EH}} = \frac{{OI}}{{OH}} = \frac{{3,6}}{6} = \frac{3}{5}\) nên EH = \(\frac{{4,8.5}}{3}\) = 8 cm.
∆OEF cân tại O (vì \(\widehat E = \widehat F = \widehat {BAO} = \widehat {ABO}\)) có OH ⊥ EF nên H là trung điểm của EF.
Vì EF = 2EH = 16 cm nên diện tích tam giác EOF là
\(\frac{1}{2}\)OH.EF = \(\frac{1}{2}\).6.16 = 48 cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Sử dụng bảng dữ liệu dưới đây để trả lời Bài 3, 4.
Có R là bán kính đường tròn, d là khoảng cách từ tâm đến đường thẳng.

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
33 Đánh giá
50%
40%
0%
0%
0%