20 câu Trắc nghiệm Toán 12 Kết nối tri thức Bài 13. Ứng dụng hình học của tích phân có đáp án
50 người thi tuần này 4.6 1 K lượt thi 20 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1
A. \[V = \pi \int\limits_a^b {{f^2}\left( x \right)dx.} \]
B. \[V = \pi \int\limits_a^b {f\left( x \right)dx.} \]
C. \[V = {\pi ^2}\int\limits_a^b {{f^2}\left( x \right)dx.} \]
D. \[V = \int\limits_a^b {{f^2}\left( x \right)dx.} \]
Lời giải
Đáp án đúng là: A
Câu 2
A. \[S = \int\limits_a^b {{f^2}\left( x \right)dx.} \]
B. \[S = \int\limits_a^b {f\left( x \right)dx.} \]
C. \[S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx.} \]
D. \[S = \pi \int\limits_a^b {\left| {f\left( x \right)} \right|dx.} \]
Lời giải
Đáp án đúng là: C
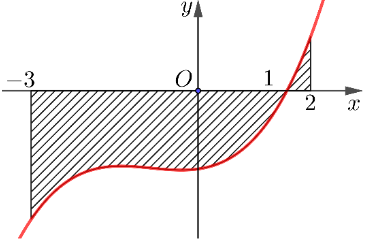
Câu 3
A. \[S = a + b.\]
B. \[S = a - b.\]
C. \[S = - a - b.\]
D. \[S = b - a.\]
Lời giải
Đáp án đúng là: D
Ta có: \[S = \int\limits_{ - 3}^2 {\left| {f\left( x \right)} \right|dx = } \int\limits_{ - 3}^1 {\left| {f\left( x \right)} \right|dx} + \int\limits_1^2 {\left| {f\left( x \right)} \right|dx} \]
\[ = - \int\limits_{ - 3}^1 {f\left( x \right)dx} + \int\limits_1^2 {f\left( x \right)dx} \]\[ = b - a.\]
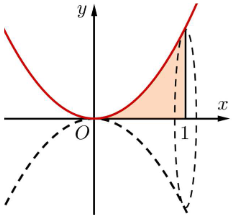
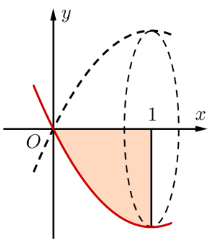
Câu 4
A. \[S = \int\limits_0^2 {{3^x}dx} .\]
B. \[S = \pi \int\limits_0^2 {{3^{2x}}dx} .\]
C. \[S = \pi \int\limits_0^2 {{3^x}dx} .\]
D. \[S = \int\limits_0^2 {{3^{2x}}dx} .\]
Lời giải
Đáp án đúng là: A
Ta có: \[S = \int\limits_0^2 {\left| {{3^x} - 0} \right|dx} = \int\limits_0^2 {{3^x}dx} .\]
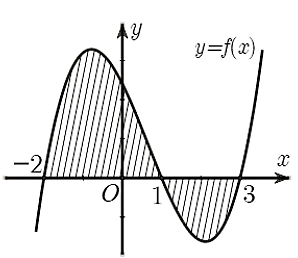
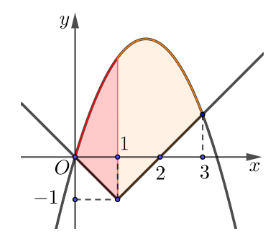
Câu 5
A. \[S = - \int\limits_{ - 2}^1 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} .\]
B. \[S = \int\limits_{ - 2}^1 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} .\]
C. \[S = - \int\limits_{ - 2}^1 {f\left( x \right)dx} + \int\limits_1^3 {f\left( x \right)dx} .\]
D. \[S = \int\limits_{ - 2}^1 {f\left( x \right)dx} + \int\limits_1^3 {f\left( x \right)dx} .\]
Lời giải
Đáp án đúng là: B
Ta có: \[S = \int\limits_{ - 2}^3 {\left| {f\left( x \right)} \right|dx = } \int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx} + \int\limits_1^3 {\left| {f\left( x \right)} \right|dx} \]
\[ = \int\limits_{ - 2}^1 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} .\]
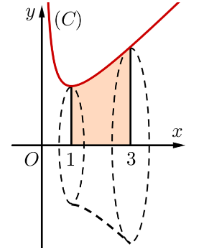
Câu 6
A. \[\frac{1}{3}.\]
B. \[\frac{2}{3}.\]
C. \[\frac{3}{2}.\]
D. \[\frac{7}{3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
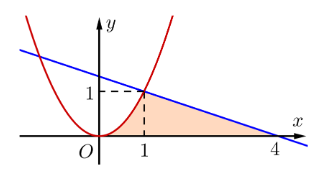
Câu 7
A. \[S = 16.\]
B. \[S = 6.\]
C. \[S = \frac{{13}}{6}.\]
D. \[S = 13.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \[V = 12\pi .\]
B. \[V = \frac{{348\pi }}{5}.\]
C. \[V = 32\pi .\]
D. \[V = 9\pi .\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
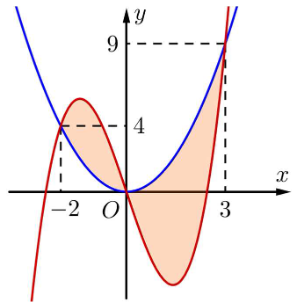
Câu 9
A. \[S = \int\limits_{ - 2}^0 {\left( {{x^3} - 6x - {x^2}} \right)} dx.\]
B. \[S = \int\limits_{ - 2}^3 {\left( {{x^3} - 6x - {x^2}} \right)} dx.\]
C. \[S = \int\limits_{ - 2}^9 {\left( {{x^2} - {x^3} + 6x} \right)} dx.\]
D. \[S = \int\limits_{ - 2}^0 {\left( {{x^3} - 6x - {x^2}} \right)} dx - \int\limits_0^3 {\left( {{x^3} - 6x - {x^2}} \right)} dx.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \[{e^2}.\]
B. \[e + 2.\]
C. \[2e.\]
D. \[e - 2.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \[V = \frac{{\pi \left( {{e^2} + 1} \right)}}{2}.\]
B. \[V = \frac{{{e^2} - 1}}{2}.\]
C. \[V = \frac{{\pi {e^2}}}{3}.\]
D. \[V = \frac{{\pi \left( {{e^2} - 1} \right)}}{2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \[V = \left( {\pi + 1} \right)\pi .\]
B. \[V = \pi - 1.\]
C. \[V = \pi + 1.\]
D. \[V = \left( {1 - \pi } \right)\pi .\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. \[\frac{\pi }{5}.\]
B. \[\frac{\pi }{3}.\]\[\]
C. \[\frac{{2\pi }}{3}.\]
D. \[\frac{{2\pi }}{5}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \[V = \frac{{8\pi }}{{15}}.\]
B. \[V = \frac{{4\pi }}{3}.\]
C. \[V = \frac{{15\pi }}{8}.\]
D. \[V = \frac{{7\pi }}{8}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. \[\frac{7}{3}.\]
B. \[\frac{{56}}{3}.\]
C. \[\frac{{39}}{2}.\]
D. \[\frac{{11}}{6}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
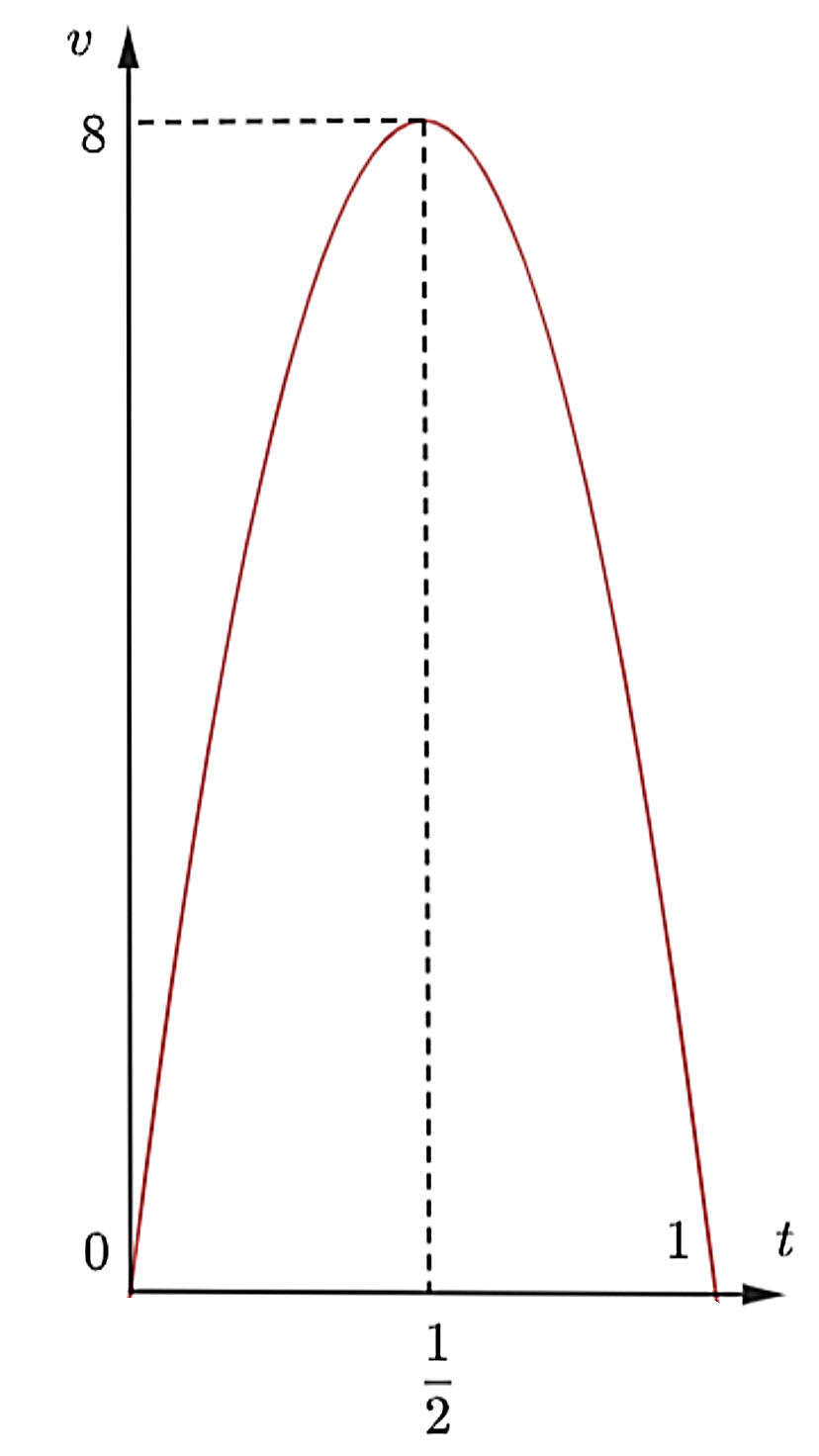
Câu 16
A. 4 km.
B. 5 km.
C. 4,5 km.
D. 5,5 km.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. \[16 < V < 17.\]
B. \[41 < V < 42.\]
C. \[13 < V < 14.\]
D. \[5 < V < 6.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. \[\frac{{13}}{2}.\]
B. \[\frac{{11}}{6}.\]
C. \[\frac{{14}}{3}.\]
D. \[\frac{{11}}{3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. \[11445000\] đồng.
B. \[4077000\] đồng.
C. \[7368000\] đồng.
D. \[11370000\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
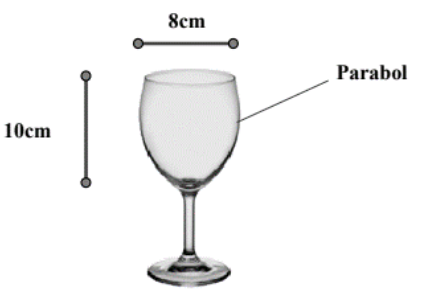
Câu 20
A. \[V \approx 320\] cm3.
B. \[V \approx 1005,31\] cm3.
C. \[V \approx 251,33\] cm3.
D. \[V \approx 502,65\] cm3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.