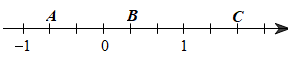Bộ 10 đề thi cuối kì 1 Toán 7 Cánh diều có đáp án - Đề 3
23 người thi tuần này 4.6 0.9 K lượt thi 18 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 9
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 8
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 7
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 6
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 5
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 3
Danh sách câu hỏi:
Câu 1
Lời giải
Đáp án đúng là: A
Số \(2,\left( 1 \right)\) là số thập phân vô hạn hữu hạn nên không phải là số hữu tỉ.
Do đó cách viết \[2,\left( 1 \right) \notin \mathbb{Q}\] là đúng.
Câu 2
Lời giải
Đáp án đúng là: B
Số đối của số hữu tỉ \(a\) là \( - a\). Số đối của \( - 1\frac{2}{5}\) là \(1\frac{2}{5}\).
Câu 3
Lời giải
Đáp án đúng là: B
Quan sát trục số ta thấy:
‒ Điểm \(A\) biểu diễn số \(\frac{{ - 2}}{3}\);
‒ Điểm \(B\) biểu diễn số \(\frac{1}{3}\);
‒ Điểm \(C\) biểu diễn số \(\frac{5}{3}\).
Câu 4
Lời giải
Đáp án đúng là: D
Ta có \[\frac{{ - 2929}}{{100}} = - 29,29\] mà \[ - 29,29 > - 30\] nên \[\frac{{ - 2929}}{{100}} > - 30\].
Vậy \(a > b\).
Câu 5
A. \(\frac{{35}}{{210}}\);
Lời giải
Đáp án đúng là: B
Ta có \(\frac{{35}}{{210}} = \frac{1}{6}\); \(\frac{{15}}{{210}} = \frac{1}{{14}}\) và \(\frac{{14}}{{210}} = \frac{1}{{15}}\). Các phân số này đều có mẫu có ước nguyên tố khác 2 và 5 nên viết được dưới dạng số thập phân vô hạn tuần hoàn.
Vì \(\frac{{21}}{{210}} = \frac{1}{{10}} = 0,1\) nên viết được dưới dạng số thập phân hữu hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
(1,5 điểm) Cho hình vẽ sau, biết \(\widehat {ABC} = 80^\circ \) và \(Am\,{\rm{//}}\,Cp\).
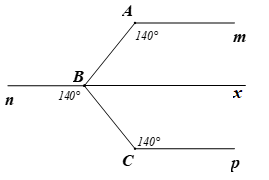
a) Vẽ lại hình (đúng số đo các góc) và viết giả thiết, kết luận của bài toán.
b) Giải thích tại sao hai đường thẳng \(Bn\) và \(Cp\) song song với nhau. Từ đó suy ra hai đường thẳng \(Am\) và \(Bn\) song song với nhau.
c) Kẻ \(Bx\) là tia đối của tia \(Bn\). Chứng minh \(Bx\) là tia phân giác của \(\widehat {ABC}\).
(1,5 điểm) Cho hình vẽ sau, biết \(\widehat {ABC} = 80^\circ \) và \(Am\,{\rm{//}}\,Cp\).

a) Vẽ lại hình (đúng số đo các góc) và viết giả thiết, kết luận của bài toán.
b) Giải thích tại sao hai đường thẳng \(Bn\) và \(Cp\) song song với nhau. Từ đó suy ra hai đường thẳng \(Am\) và \(Bn\) song song với nhau.
c) Kẻ \(Bx\) là tia đối của tia \(Bn\). Chứng minh \(Bx\) là tia phân giác của \(\widehat {ABC}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.