Đề cương ôn tập giữa kì 1 Toán 8 Chân trời sáng tạo cấu trúc mới (Đúng sai - Trả lời ngắn) có đáp án
27 người thi tuần này 4.6 606 lượt thi 20 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
Đáp án: a) S. b) Đ. c) S. d) Đ.
⦁ Thay \(x = 1\,;\,\,y = - 1\) vào biểu thức \(P\), ta có:
\(P = {1^2} - 4 \cdot 1 \cdot \left( { - 1} \right) + 9 = 1 + 4 + 9 = 15.\)
Vậy với \(x = 1\,;\,\,y = 0\) thì \(P = 10\). Do đó ý a) sai.
⦁ Đa thức \(Q = - 6xy - 4{y^2} + 9\) có bậc là 2. Do đó ý b) đúng.
⦁ Ta có \(P - A = Q\)
Suy ra \(A = P - Q\)
\( = {x^2} - 4xy + 9 - \left( { - 6xy - 4{y^2} + 9} \right)\)
\( = {x^2} - 4xy + 9 + 6xy + 4{y^2} - 9\)
\( = {x^2} + 2xy + 4{y^2}\)
Như vậy \(A = {x^2} + 2xy + 4{y^2}.\) Do đó ý c) sai.
⦁ Ta có: \[M = \left( {x - 2y} \right)A - {x^3} + 5\]
\( = \left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right) - {x^3} + 5\)
\[ = x\left( {{x^2} + 2xy + 4{y^2}} \right) - 2y\left( {{x^2} + 2xy + 4{y^2}} \right) - {x^3} + 5\]
\[ = {x^3} + 2{x^2}y + 4x{y^2} - 2{x^2}y - 4x{y^2} - 8{y^3} - {x^3} + 5\]
\[ = {x^3} - 8{y^3} - {x^3} + 5\]\[ = - 8{y^3} + 5\].
Như vậy, giá trị của biểu thức \(M\) không phụ thuộc vào giá trị của biến \(x.\) Do đó ý d) đúng.
Vậy: a) S. b) Đ. c) S. d) Đ.
Câu 2
Cho hai đa thức \(A = {x^2} - 4xy - 4\) và \(B = 2{x^2} - 3xy + {y^2} - 4.\)
Đa thức \(M\) và \(P\) thỏa mãn
a) Hạng tử tự do của đa thức \(A\) là \( - 4\).
b) Với \(x = 1\,;\,\,y = 0\) thì giá trị của biểu thức \(B\) bằng \( - 2.\)
c) \(M = {x^2} + 7xy + {y^2}.\)
d) Giá trị của biểu thức \(P\) không phụ thuộc vào biến \(y\).
Cho hai đa thức \(A = {x^2} - 4xy - 4\) và \(B = 2{x^2} - 3xy + {y^2} - 4.\)
Đa thức \(M\) và \(P\) thỏa mãn
a) Hạng tử tự do của đa thức \(A\) là \( - 4\).
b) Với \(x = 1\,;\,\,y = 0\) thì giá trị của biểu thức \(B\) bằng \( - 2.\)
c) \(M = {x^2} + 7xy + {y^2}.\)
d) Giá trị của biểu thức \(P\) không phụ thuộc vào biến \(y\).
Lời giải
Hướng dẫn giải
Đáp án: a) Đ. b) S. c) S. d) Đ.
⦁ Đa thức \(A\) có hạng tử tự do là \( - 4\). Do đó ý a) đúng.
⦁ Thay \(x = 1\,;\,\,y = 0\) vào biểu thức \(B\), ta có:
\(B = 2 \cdot {1^2} - 3 \cdot 1 \cdot 0 + {0^2} - 4 = 2 - 4 = - 2.\)
Vậy với \(x = 1\,;\,\,y = 0\) thì \(N = - 2\). Do đó ý b) sai.
⦁ Ta có: \(B = A + M\)
Suy ra \(M = B - A\)
\( = 2{x^2} - 3xy + {y^2} - 4 - \left( {{x^2} - 4xy - 4} \right)\)
\( = 2{x^2} - 3xy + {y^2} - 4 - {x^2} + 4xy + 4\)
\( = {x^2} + xy + {y^2}.\)
Như vậy \(M = {x^2} + xy + {y^2}.\) Do đó ý c) sai.
⦁ Ta có \[P = \left( {x - 3} \right)M - y - \left( {x + y} \right)\left( {xy - 3y} \right)\]
\( = \left( {x - 3} \right)\left( {{x^2} + xy + {y^2}} \right) - \left( {{x^2}y - 3xy + x{y^2} - 3{y^2}} \right)\)
\[ = x\left( {{x^2} + xy + {y^2}} \right) - 3\left( {{x^2} + xy + {y^2}} \right) - {x^2}y + 3xy - x{y^2} + 3{y^2}\]
\[ = {x^3} + {x^2}y + x{y^2} - 3{x^2} - 3xy - 3{y^2} - {x^2}y + 3xy - x{y^2} + 3{y^2}\]
\[ = {x^3} - 3{x^2}\].
Như vậy, giá trị của biểu thức \(P\) không phụ thuộc vào giá trị của biến \(y.\) Do đó ý d) đúng.
Vậy: a) Đ. b) S. c) S. d) Đ.
Lời giải
Hướng dẫn giải
Đáp án: a) S. b) Đ. c) Đ. d) S.
⦁ Biểu thức \(M\) là đa thức có bậc 24. Do đó ý a) sai.
⦁ Thay \(x = 0\,;\,y = - 2\) vào biểu thức \(N\), ta có:
\(N = - 22 \cdot 0 \cdot {\left( { - 2} \right)^3} - 42 \cdot \left( { - 2} \right) - 1 = 0 + 84 - 1 = 83.\)
Vậy với \(x = 0\,;\,y = - 2\) thì \(N = 83\). Do đó ý b) đúng.
⦁ Ta có \(M - N = \left( {23{x^{23}}y - 22x{y^{23}} + 21y - 1} \right) - \left( { - 22x{y^3} - 42y - 1} \right)\)
\( = 23{x^{23}}y - 22x{y^{23}} + 21y - 1 + 22x{y^3} + 42y + 1\)
\( = 23{x^{23}}y - 22x{y^{23}} + 22x{y^3} + \left( {21y + 42y} \right) + \left( { - 1 + 1} \right)\)
\( = 23{x^{23}}y - 22x{y^{23}} + 22x{y^3} + 63y\).
Do đó ý c) đúng.
⦁ Từ \(M - N - P = 63y + 1\) suy ra
\(P = \left( {M - N} \right) - \left( {63y + 1} \right)\)
\( = \left( {23{x^{23}}y - 22x{y^{23}} + 22x{y^3} + 63y} \right) - \left( {63y + 1} \right)\)
\( = 23{x^{23}}y - 22x{y^{23}} + 22x{y^3} + 63y - 63y - 1\)
\( = 23{x^{23}}y - 22x{y^{23}} + 22x{y^3} - 1\).
Như vậy, \(P = 23{x^{23}}y - 22x{y^{23}} + 22x{y^3} - 1\). Do đó ý d) sai.
Vậy: a) S. b) Đ. c) Đ. d) S.
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) S b) Đ c) Đ d) S
⦁ Ta có \(45{x^6}{y^3}:A = 5x{y^2}\).
Suy ra \(A = 45{x^6}{y^3}:5x{y^2} = 9{x^3}y\).
Như vậy, biểu thức \(A\) là đơn thức bậc 4. Do đó ý a) sai.
⦁ Thay \(x = - 1\,;\,\,y = 2\) vào biểu thức \(A\), ta có: \(A = 9 \cdot {\left( { - 1} \right)^3} \cdot 2 = - 9 \cdot 2 = - 18.\)
Vậy với \(x = - 1\,;\,\,y = 2\) thì \(A = - 18\). Do đó ý b) đúng.
⦁ Với \(A = 9{x^3}y\), ta có \(\left( {B + 7{x^4}{y^2}} \right):9{x^3}y = 3x{y^2} + 2xy\)
Suy ra \(B + 7{x^4}{y^2} = 9{x^3}y\left( {3x{y^2} + 2xy} \right) = 27{x^4}{y^4} + 18{x^4}{y^2}.\)
Do đó \(B = 27{x^4}{y^4} + 18{x^4}{y^2} - 7{x^4}{y^2} = 27{x^4}{y^4} + 11{x^4}{y^2}\).
Như vậy \(B = 27{x^4}{y^4} + 11{x^4}{y^2}\). Do đó ý c) đúng.
⦁ Ta có \(A \cdot B = 9{x^3}y \cdot \left( {27{x^4}{y^4} + 11{x^4}{y^2}} \right)\)
\( = 9{x^3}y \cdot 27{x^4}{y^4} + 9{x^3}y \cdot 11{x^4}{y^2}\)
\( = 243{x^7}{y^5} + 99{x^7}{y^3}.\)
Như vậy, tích của hai biểu thức \(A\) và \(B\) là \(243{x^7}{y^5} + 99{x^7}{y^3}.\) Do đó ý d) sai.
Vậy: a) S. b) Đ. c) Đ. d) S.
Lời giải
Hướng dẫn giải
Đáp án: a) Đ. b) Đ. c) S. d) S.
⦁ Thay \[x = - 1\,;\,\,y = 1\] vào biểu thức \(A\), ta có:
\(A = 3 \cdot {\left( { - 1} \right)^2} \cdot 1 - 2 \cdot \left( { - 1} \right) \cdot {1^2} - 4 \cdot \left( { - 1} \right) \cdot 1 + 1 = 3 + 2 + 4 = 9.\)
Vậy với \[x = - 1\,;\,\,y = 1\] thì \(A = 9\). Do đó ý a) đúng.
⦁ Ta có \(B - A = - 2{x^3}y + 7{x^2}y + 3xy.\)
Suy ra \(B = - 2{x^3}y + 7{x^2}y + 3xy + A\)
\( = - 2{x^3}y + 7{x^2}y + 3xy + \left( {3{x^2}y - 2x{y^2} - 4xy + 1} \right)\)
\( = - 2{x^3}y + 7{x^2}y + 3xy + 3{x^2}y - 2x{y^2} - 4xy + 1\)
\( = - 2{x^3}y + \left( {7{x^2}y + 3{x^2}y} \right) - 2x{y^2} + \left( {3xy - 4xy} \right) + 1\)
\( = - 2{x^3}y + 10{x^2}y - 2x{y^2} - xy + 1\).
Khi đó, đa thức \(B\) sau khi thu gọn có 5 hạng tử. Do đó ý b) đúng.
⦁ Ta có \(A + M = 3{x^2}{y^2} - 5{x^2}y + 8xy\).
Suy ra \(M = 3{x^2}{y^2} - 5{x^2}y + 8xy - A\)
\( = 3{x^2}{y^2} - 5{x^2}y + 8xy - \left( {3{x^2}y - 2x{y^2} - 4xy + 1} \right)\)
\( = 3{x^2}{y^2} - 5{x^2}y + 8xy - 3{x^2}y + 2x{y^2} + 4xy - 1\)
\( = 3{x^2}{y^2} - \left( {5{x^2}y + 3{x^2}y} \right) + 2x{y^2} + \left( {8xy + 4xy} \right) - 1\)
\( = 3{x^2}{y^2} - 8{x^2}y + 2x{y^2} + 12xy - 1\).
Khi đó, đa thức \(M\) có bậc là 4. Do đó ý c) sai.
⦁ Tổng của hai đa thức \(B\) và \(M\) là:
\[B + M = \left( { - 2{x^3}y + 10{x^2}y - 2x{y^2} - xy + 1} \right) + \left( {3{x^2}{y^2} - 8{x^2}y + 2x{y^2} + 12xy - 1} \right)\]
\[ = - 2{x^3}y + 10{x^2}y - 2x{y^2} - xy + 1 + 3{x^2}{y^2} - 8{x^2}y + 2x{y^2} + 12xy - 1\]
\[ = - 2{x^3}y + 3{x^2}{y^2} + \left( {10{x^2}y - 8{x^2}y} \right) + \left( {2x{y^2} - 2x{y^2}} \right) + \left( {12xy - xy} \right) + \left( {1 - 1} \right)\]
\[ = - 2{x^3}y + 3{x^2}{y^2} + 2{x^2}y + 11xy\].
Như vậy, tổng của hai đa thức \(B\) và \(M\) có hạng tử tự do là 0. Do đó ý d) sai.
Vậy: a) Đ. b) Đ. c) S. d) S.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Một bể kính hình hộp chữ nhật có hai cạnh đáy là \(60{\rm{ cm}}\) và \(30{\rm{ cm}}{\rm{.}}\) Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270{\rm{ c}}{{\rm{m}}^2}\), chiều cao \(30{\rm{ cm}}{\rm{.}}\) Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mức nước là \(60{\rm{ cm}}{\rm{.}}\)
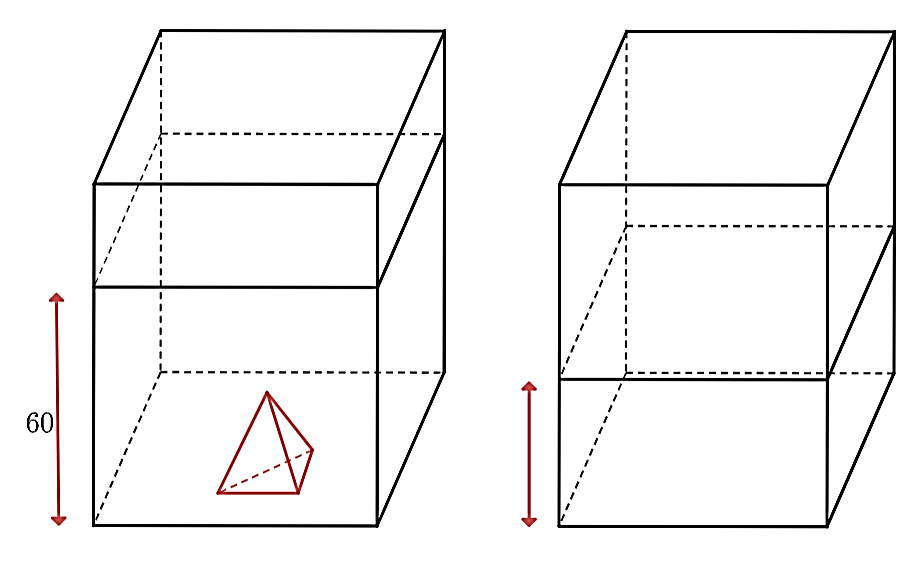
a) Diện tích đáy của bể hình hộp chữ nhật là \(180{\rm{ c}}{{\rm{m}}^{\rm{2}}}\).
b) Thể tích khối đá hình chóp tam giác đều là: \(2{\rm{ }}700{\rm{ c}}{{\rm{m}}^3}.\)
c) Thể tích khối nước là \(108{\rm{ }}000{\rm{ c}}{{\rm{m}}^2}\).
d) Khi lấy khối đá ra thì mực nước của bể cao 56 cm.
Một bể kính hình hộp chữ nhật có hai cạnh đáy là \(60{\rm{ cm}}\) và \(30{\rm{ cm}}{\rm{.}}\) Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270{\rm{ c}}{{\rm{m}}^2}\), chiều cao \(30{\rm{ cm}}{\rm{.}}\) Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mức nước là \(60{\rm{ cm}}{\rm{.}}\)

a) Diện tích đáy của bể hình hộp chữ nhật là \(180{\rm{ c}}{{\rm{m}}^{\rm{2}}}\).
b) Thể tích khối đá hình chóp tam giác đều là: \(2{\rm{ }}700{\rm{ c}}{{\rm{m}}^3}.\)
c) Thể tích khối nước là \(108{\rm{ }}000{\rm{ c}}{{\rm{m}}^2}\).
d) Khi lấy khối đá ra thì mực nước của bể cao 56 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm,}}\)chiều cao \(90{\rm{ cm}}\) (như hình vẽ).
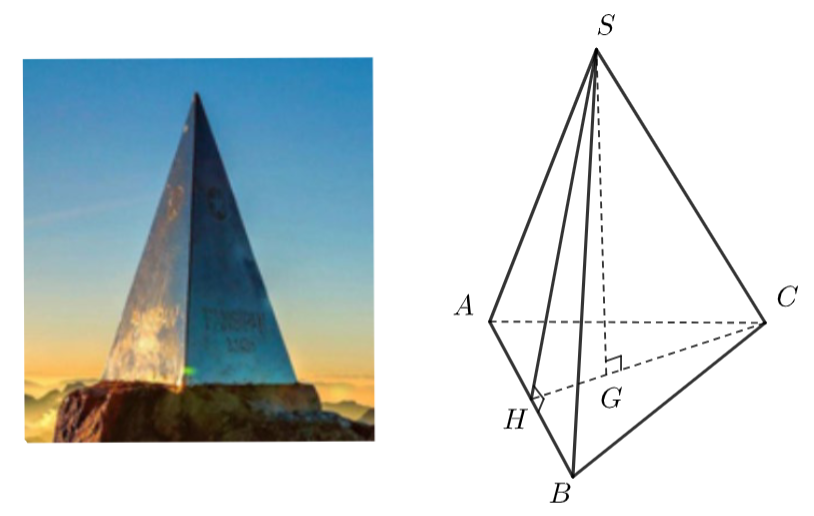
a) Tam giác đều \(ABC\) có \(CH\) là đường trung tuyến.
b) Độ dài đường trung tuyến \(CH\) bằng \(30\sqrt 3 {\rm{ cm}}\).
c) Độ dài cạnh \(SH\) nhỏ hơn độ dài cạnh \(CH\).
d) Diện tích xung quanh của hình chóp là \(8635{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\)
Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm,}}\)chiều cao \(90{\rm{ cm}}\) (như hình vẽ).

a) Tam giác đều \(ABC\) có \(CH\) là đường trung tuyến.
b) Độ dài đường trung tuyến \(CH\) bằng \(30\sqrt 3 {\rm{ cm}}\).
c) Độ dài cạnh \(SH\) nhỏ hơn độ dài cạnh \(CH\).
d) Diện tích xung quanh của hình chóp là \(8635{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![b) Thể tích của khối bê tông là \(1,2{\rm{ c}}{{\rm{m}}^3}.\) c) Khối lượng xi măng cần dùng để làm khối bê tông đó là \[0,5\] tấn. d) Lượng nước cần dùng để làm khối bê tông đó là \(0,185{\rm{ }}{{\rm{m}}^3}.\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/20-1758419224.png)

![Bộ nam châm xếp hình có dạng hình chóp tam giác đều (như hình ảnh) có độ dài cạnh đáy khoảng 6 cm và mặt bên có đường cao khoảng 7 cm. Tính diện tích xung quanh bộ nam châm xếp hình đó theo đơn vị \[{\rm{c}}{{\rm{m}}^{\rm{2}}}\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/24-1758419460.png)
![Bác Mai muốn may một cái lều cắm trại bằng vải bạt có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2,5 m, chiều cao của cái lều trại là 3 m. Tính thể tích khoảng không bên trong lều theo đơn vị \[{\rm{c}}{{\rm{m}}^3}.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/25-1758419488.png)
![Cho hình vẽ, biết \[\widehat B + \widehat D = 135^\circ \,,\,\,\widehat {BAD} = \frac{{7x}}{2}\]. Tính số đo góc \[\widehat {{C_1}}\] (đơn vị: độ). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/29-1758419576.png)