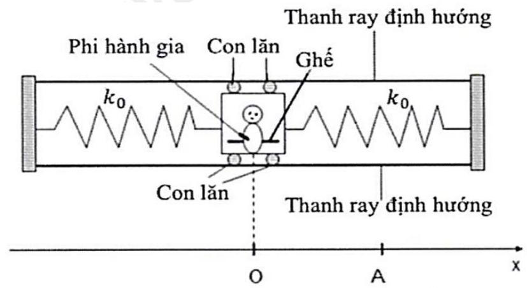
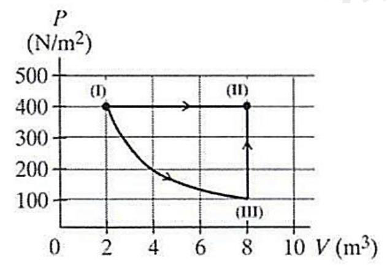
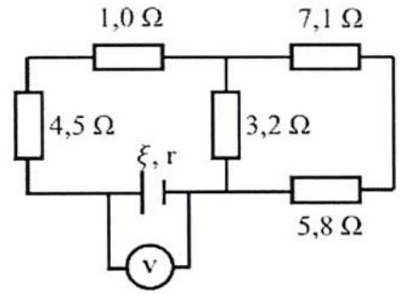
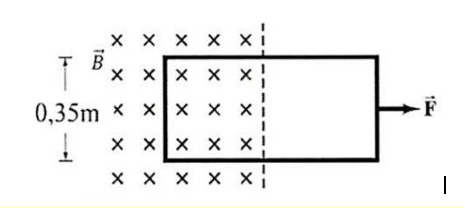
Đề thi tham khảo ĐGNL - Đại học Sư Phạm Hà Nội có đáp án
6 người thi tuần này 4.6 6 lượt thi 21 câu hỏi 45 phút
🔥 Đề thi HOT:
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 2)
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 1)
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Thuận Thành - Bắc Ninh - Lần 1 có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 13)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Phương pháp:
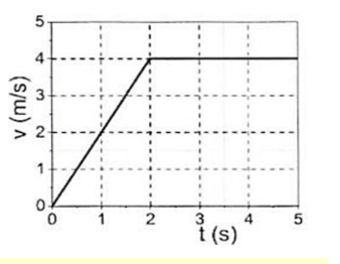
Phân tích đồ thị hình vẽ để xác định được thời gian và vận tốc tương ứng.
Xác định quãng đường đi được trong từng khoảng thời gian.
Công thức tính tốc độ trung bình: \({v_{tb}} = \frac{S}{t}\)
Cách giải:
Từ đồ thị ta có:
Trong 2s đầu tiên tốc độ của vận động viên tăng từ 0 lên 4m/s
Quãng đường vận động viên di chuyển là:
\({s_1} = {v_0}t + \frac{1}{2}a{t^2} = \frac{1}{2}.\frac{4}{2}{.2^2} = 4\left( {\rm{m}} \right)\)
Trong 3s tiếp theo tốc độ không đổi là 4m/s
Quãng đường vận động viên di chuyển là:
\({s_2} = v.t = 4.3 = 12\left( {\rm{m}} \right)\)
Tốc độ trung bình của vận động viên:
\({v_{tb}} = \frac{s}{t} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{4 + 12}}{5} = 3,2\left( {{\rm{m/s}}} \right)\)
Chú ý khi giải:
Ngoài cách tính quãng đường trên thì mình có thể xác định quãng đường từ đồ thị: quãng đường chính là diện tích của hình phẳng được tạo bởi trục hoành trong đồ thị \({\rm{v}} - {\rm{t}}\), trong bài trên chính là diện tích của hình thang được tính như sau:
\(s = \frac{{\left( {3 + 5} \right).4}}{2} = 16\left( {\rm{m}} \right)\)
Chọn A.
Lời giải
Phương pháp:
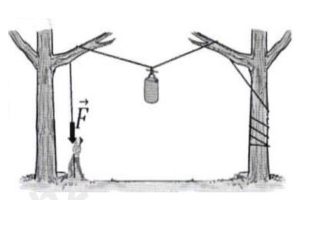
Phân tích các lực tác dụng lên vật.
Sử dụng điều kiện cân bằng của vật
Cách giải:
Giả sử xét vật tại vị trí cân bằng
Ta có các lực tác dụng lên vật:
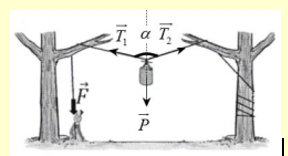
Khi balo ở vị trí cân bằng thì:
\(\vec P + {\vec T_1} + {\vec T_2} = \vec 0\)
Khi cân bằng thì: \({T_1} = {T_2} = T\)
\( \Rightarrow P = 2T.{\rm{cos}}\frac{\alpha }{2}\) (1)
Mặt khác ta có: \({\rm{F}} = {\rm{T}}\) (2) vì lực căng trên cùng sợi dây là như nhau.
Từ (1) và ( 2 ) suy ra:
\(F = \frac{{mg}}{{2{\rm{cos}}\frac{\alpha }{2}}}\)
Kéo với lực \(\vec F\) từ vị trí cân bằng \( \to \) vật lên trên \( \to \) góc \(\alpha \) tăng lên \( \to {\rm{cos}}\alpha \) càng nhỏ \( \to {\rm{F}}\) càng lớn
Từ đó ta có: vật càng lên cao dây càng căng và lực kéo càng phải tăng lên và dây luôn bị trùng ở vị trí treo balo.
Lời giải
Phương pháp:
Sử dụng lí thuyết về động năng và thế năng
Công thức tính động năng: \({W_d} = \frac{1}{2}m{v^2}\)
Công thức tính thế năng: \({W_t} = mgh\)
Cách giải:
Động năng của vật được xác định: \({W_d} = \frac{1}{2}m{v^2}\)
\( \to \) Khi người đẩy vật lên mặt phẳng nghiêng với tốc độ không đổi, điều này có nghĩa là vận tốc của vật không đổi. Do đó, động năng của vật không đổi
Thế năng vật được xác định: \({W_t} = mgh\)
\( \to \) khi vật di chuyển lên cao hơn, thế năng của vật tăng
Chọn C.
Lời giải
Phương pháp:
Sử dụng định luật Newton II để xác định lực tác dụng: F = ma
Áp dụng công thức tính gia tốc: \(a = \frac{{{\rm{\Delta }}v}}{{{\rm{\Delta }}t}}\)
Cách giải:
Chọn chiều dương là chiều từ trên xuống dưới.
Gọi vận tốc ngay trước khi va chạm là \({\vec v_1}\) và ngay sau va chạm là \(\overrightarrow {{v_2}} \)
Trong quá trình va chạm ta có: \(\overrightarrow {{v_1}} \) hướng xuống và \(\overrightarrow {{v_2}} \) hướng lên.
Độ biến thiên vận tốc của vật là:
\(\left| {{\rm{\Delta }}v} \right| = \left| {{v_2} - {v_1}} \right| = \left| { - 6,25 - 6,50} \right| = 12,75{\rm{\;m}}/{\rm{s}}\)
Áp dụng công thức định luật II Newton ta có lực tác dụng:
\(\left| F \right| = m\left| a \right| = m.\frac{{\left| {{\rm{\Delta }}v} \right|}}{{{\rm{\Delta }}t}} = 0,15.\frac{{12,75}}{{{{0,25.10}^{ - 1}}}} = 76,5\left( {\rm{N}} \right)\)
Lời giải
Phương pháp:
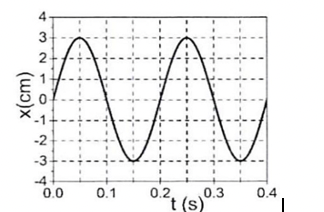
Phân tích đồ thị hình vẽ, xác định chu kì sóng.
Sử dụng công thức: \(f = \frac{1}{T}\)
Cách giải:
Từ đồ thị ta có chu kì sóng truyền:
\({\rm{T}} = 0,1.2 = 0,2\left( {\rm{s}} \right)\)
Tần số của sóng truyền đi là:
\(f = \frac{1}{T} = \frac{1}{{0,2}} = 5{\rm{\;Hz}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.