Giải SBT Toán 8 Cánh diều Bài 4. Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử có đáp án
38 người thi tuần này 4.6 886 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 10 (có đáp án)
Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 8 (có đáp án)
Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 1
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
a) \(25{x^2} - \frac{1}{4} = {\left( {5x} \right)^2} - {\left( {\frac{1}{2}} \right)^2} = \left( {5x - \frac{1}{2}} \right)\left( {5x + \frac{1}{2}} \right)\).
b) 36x2 + 12xy + y2 = (6x)2 + 2.6.1.xy + y2 = (6x + y)2.
c) \(\frac{{{x^3}}}{2} + 4 = \frac{1}{2}\left( {{x^3} + {2^3}} \right) = \frac{1}{2}\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)\).
d) 27y3 + 27y2 + 9y + 1 = (3y)3 + 3.(3y)2.1 + 3.3y.12 + 13 = (3y + 1)3.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
a) x3(13xy ‒ 5) ‒ y3(5 ‒ 13xy)
= x3(13xy ‒ 5) + y3(13xy ‒ 5)
= (13xy ‒ 5)(x3 + y3)
= (13xy ‒ 5)(x + y)(x2 ‒ xy + y2).
b) 8x3yz + 12x2yz + 6xyz + yz
= yz(8x3 + 12x2 + 6x + 1)
= yz[(2x)3 + 3.(2x)2.1 + 3.2x.12 + 13)]
= yx(2x + 1)3.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
a) Ta có: \(A = {x^2} + xy + \frac{{{y^2}}}{4} = {x^2} + 2 \cdot x \cdot \frac{y}{2} + {\left( {\frac{y}{2}} \right)^2} = {\left( {x + \frac{y}{2}} \right)^2}\).
Thay \(x + \frac{y}{2} = 100\) vào biểu thức trên ta có: A = 1002 = 10 000.
b) Ta có: B = 25x2z ‒ 10xyz + y2z
= z(25x2 ‒ 10xy + y2)
= z[(5x)2 ‒ 2.5x.y + y2)]
= z(5x ‒ y)2.
Thay 5x ‒ y = ‒20 và z = ‒5 vào biểu thức trên ta có:
B = ‒5.(‒20)2 = –5.400 = ‒2 000.
c) Ta có: C = x3yz + 3x2y2z + 3xy3z + y4z
= yz(x3 + 3x2y + 3xy2 + y3)
= yz(x + y)3.
Thay x + y = ‒0,5 và yz = 8 vào biểu thức trên ta có:
\[C = 8.{\left( { - 0,5} \right)^3} = 8.{\left( { - \frac{1}{2}} \right)^3} = 8.\left( { - \frac{1}{8}} \right) = - 1.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
Trước hết, ta chứng minh (x5 ‒ x) ⋮ 5.
Ta có: x5 ‒ x = x(x4 ‒ 1) = x(x2 ‒ 1)(x2 + 1) = x(x ‒ 1)(x + 1)(x2 + 1)
• Nếu x = 5k thì x ⋮ 5.
Khi đó x(x ‒ 1)(x + 1)(x2 + 1) ⋮ 5 hay (x5 ‒ x) ⋮ 5.
• Nếu x = 5k + 1 thì x ‒ 1 = 5k ⋮ 5 .
Khi đó x(x ‒ 1)(x + 1)(x2 + 1) ⋮ 5 hay (x5 ‒ x) ⋮ 5.
• Nếu x = 5k + 2 thì x2 + 1 = (5k + 2)2 + 1 = 25k2 + 20k + 5 ⋮ 5.
Khi đó x(x ‒ 1)(x + 1)(x2 + 1) ⋮ 5 hay (x5 ‒ x) ⋮ 5.
• Nếu x = 5k + 3 thì x2 + 1 = (5k + 3)2 + 1 = 25k2 + 30k + 10 ⋮ 5.
Khi đó x(x ‒ 1)(x + 1)(x2 + 1) ⋮ 5 hay (x5 ‒ x) ⋮ 5.
• Nếu x = 5k + 4 thì x + 1 = 5k + 5 ⋮ 5.
Khi đó x(x ‒ 1)(x + 1)(x2 + 1) ⋮ 5 hay (x5 ‒ x) ⋮ 5.
Do đó x5 ‒ x ⋮ 5 với mọi số nguyên x.
Ta có: x5 ‒ x ⋮ 5; 15x2 ⋮ 5; 5 ⋮ 5 nên x5 ‒ 15x2 ‒ x + 5 ⋮ 5 với mọi số nguyên x.
Vậy B chia hết cho 5 với mọi số nguyên x.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
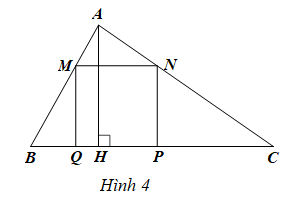
a) Diện tích của tam giác ABC là:
\[\frac{1}{2}.AH.BC = \frac{1}{2}.x.2x = {x^2}\](dm2)
Diện tích hình vuông MNPQ là:
MN2 = y2 (dm2)
Vì vậy, tổng diện tích của các tam giác AMN, BMQ, CNP là:
S = x2 ‒ y2 (dm2)
b) Từ câu a, ta có
S = x2 ‒ y2 = (x ‒ y)(x + y)
Thay x – y = 2 và x + y = 10 vào S ta được:
S = 2.10 = 20 (dm2).
Vậy tổng diện tích của các tam giác AMN, BMQ, CNP là 20 dm2.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập