Bài 8: Đường tròn

a) Vẽ đường tròn (C; 2cm)

b)

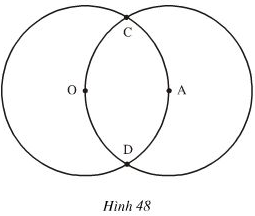
Vì hai đường tròn (O; 2cm) và (A; 2cm) cắt nhau tại C nên:

- C thuộc (O; 2cm) ⇒ OC = 2cm do đó O thuộc (C; 2cm)

- C thuộc (A; 2cm) ⇒ AC = 2cm do đó A thuộc (C; 2cm)

Vậy đường tròn (C; 2cm) đi qua hai điểm O và A.

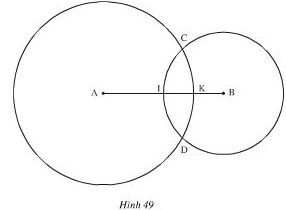
a) (A; 3cm) và (B; 2cm) cắt nhau tại C; D nên:

+ C, D nằm trên đường tròn (A; 3cm), suy ra AC = AD = 3cm.

+ C, D nằm trên đường tròn (B; 2cm), suy ra BC = BD = 2cm.

b) Đường tròn (B; 2cm) cắt đoạn AB tại I nên:

+ I nằm trên đường tròn (B; 2cm), suy ra BI = 2cm.

+ I nằm trên đoạn thẳng AB, suy ra IA + IB = AB.

Mà BI = 2cm; AB = 4cm nên AI = 2cm. Do đó BI = AI.

Kết hợp với I nằm trên đoạn thẳng AB suy ra I là trung điểm AB.

c) Đường tròn (A; 3cm) cắt đoạn AB tại K nên K thuộc đường tròn (A ; 3cm) , suy ra AK = 3cm.

Trên đoạn thẳng AB có AI < AK nên I nằm giữa A và K.

Do đó AI + IK = AK.

Mà AK = 3cm; AI = 2cm nên IK = 1cm

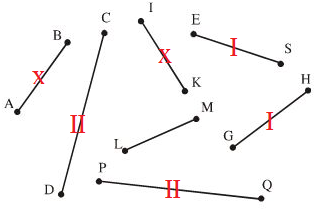
Cách so sánh: Dùng compa với độ mở sao cho hai mũi nhọn compa trùng với hai đầu của một đoạn thẳng. Với cùng độ mở đó ta có thể so sánh với độ dài đoạn thẳng thứ hai.

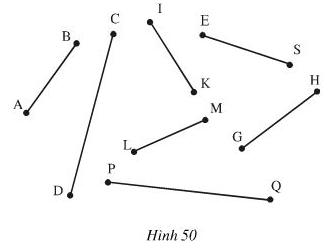
Kết quả so sánh: LM < AB = IK < ES = GH < CD = PQ

Đánh dấu như trong hình:

Chúng ta có 3 cặp đoạn thẳng bằng nhau: AB = IK; ES = GH; CD = PQ

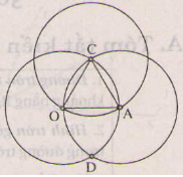
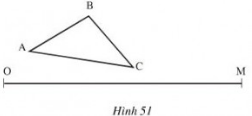
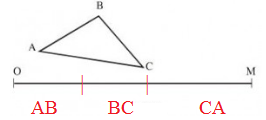
- So sánh bằng mắt: AB + BC + AC = OM

- Kiểm tra (bằng thước đo hay compa): Trên tia OM kể từ O ta đặt liên tiếp ba đoạn thẳng có độ dài lần lượt bằng AB, BC, CA. Ta thấy điểm cuối trùng với M.

Vậy AB + BC + AC = OM

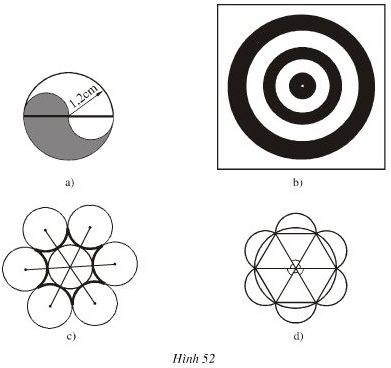
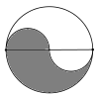
a)

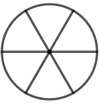
+ Vẽ đường tròn bán kính 1,2cm.

+ Vẽ một đường kính của đường tròn.

+ Xác định trung điểm của hai bán kính. Vẽ hai cung tròn có bán kính bằng một nửa bán kính của đường tròn ban đầu.

+ Tô màu như hình vẽ.

b) Trước hết vẽ hình vuông. Lấy giao điểm của hai đường chéo làm tâm vẽ 5 đường tròn có bán kính lần lượt bằng bán kính của 5 đường tròn đã cho.

c)

+ Vẽ đường tròn có bán kính bằng

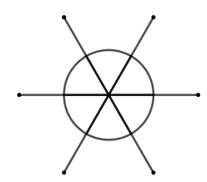
+ Chia đường tròn thành 6 phần bằng nhau bằng cách vẽ các đường kính tạo với nhau 1 góc 600.

+ Kéo dài các đường kính, trên các đường kéo dài đó lấy các điểm sao cho độ dài đoạn thẳng từ tâm đến các điểm đó bằng hai lần bán kính đường tròn.

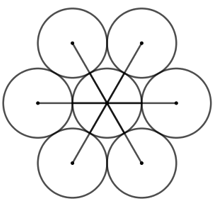
+ Vẽ các đường tròn tâm là các điểm vừa lấy, bán kính bằng bán kính đường tròn ban đầu.

+ Dùng bút nét to vẽ lại các cung tròn được tô đậm như hình dưới

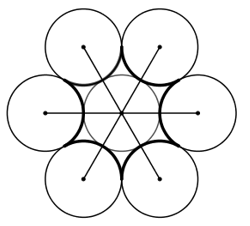
d) + Vẽ đường tròn đường kính … và chia thành 6 phần bằng nhau như phần c)

+ Nối các đoạn thẳng như hình vẽ.

+ Xác định trung điểm các đoạn thẳng vừa vẽ để làm tâm đường tròn.

+ Vẽ các nửa đường tròn.