Bài 5: Phép cộng và phép nhân

Bài 5: Phép cộng và phép nhân

Đề số 1

Bài 5: Phép cộng và phép nhân

2635 lượt xem
28 câu hỏi

Câu 1:

Điền vào chỗ trống:

a 12 21 1

b 5 0 48 15

a + b

a . b 0

(1) (2) (3) (4)

Câu 2:

Điền vào chỗ trống: Tích của một số với 0 thì bằng …

Câu 3:

Điền vào chỗ trống: Nếu tích của hai thừa số mà bằng 0 thì có ít nhất một thừa số bằng …

Câu 4:

Tính nhanh: 46 + 17 + 54;

Câu 5:

Tính nhanh: 4.37.25;

Câu 6:

Tính nhanh: 87.36 + 87.64;

Câu 7:

Cho các số liệu về quãng đường bộ:

      Hà Nội – Vĩnh Yên   : 54km

      Vĩnh Yên – Việt Trì : 19km

      Việt Trì – Yên Bái : 82km

Tính quãng đường một ô tô đi từ Hà Nội lên Yên Bái qua Vĩnh Yên và Việt Trì.

Câu 8:

Áp dụng các tính chất của phép cộng và phép nhân để tính nhanh: 86 + 357 + 14

Câu 9:

Áp dụng các tính chất của phép cộng và phép nhân để tính nhanh: 72 + 69 + 128

Câu 10:

Áp dụng các tính chất của phép cộng và phép nhân để tính nhanh: 25.5.4.27.2

Câu 11:

Áp dụng các tính chất của phép cộng và phép nhân để tính nhanh: 28.64 + 28.36

Câu 12:

Trên hình 12, đồng hồ chỉ 9 giờ 18 phút, hai kim đồng hồ chia mặt đồng hồ thành hai phần, mỗi phần có sáu số. Tính tổng các số ở mỗi phần, em có nhận xét gì?

Hình 12

Câu 13:

Điền vào chỗ trống trong bảng thanh toán sau:

Số thứ tự Loại hàng Số lượng (quyển) Giá đơn vị (đồng) Tổng số tiền (đồng)

1 Vở loại 1 35 2000 ...

2 Vở loại 2 42 1500 ...

3 Vở loại 3 38 1200 ...

Cộng: ...

Câu 14:

Tìm số tự nhiên x, biết: (x - 34).15 = 0

Câu 15:

Tìm số tự nhiên x, biết: 18.(x - 16) = 18

Câu 16:

Tính nhanh: 135 + 360 + 65 + 40

Câu 17:

Tính nhanh: 463 + 318 + 137 + 22

Câu 18:

Tính nhanh: 20 + 21 + 22 + ... + 29 + 30

Câu 19:

Có thể tính nhanh tổng 97 + 19 bằng cách áp dụng tính chất kết hợp của phép cộng:

97 + 19 = (97 + 3) + 16 = 100 + 16 = 116

Hãy tính nhanh các tổng sau bằng cách làm tương tự như trên: 996 + 45

Câu 20:

Có thể tính nhanh tổng 97 + 19 bằng cách áp dụng tính chất kết hợp của phép cộng:

97 + 19 = (97 + 3) + 16 = 100 + 16 = 116

Hãy tính nhanh các tổng sau bằng cách làm tương tự như trên: 37 + 198

Câu 21:

Cho dãy số sau 1, 1, 2, 3, 5, 8, ...

Trong dãy số trên mỗi số (kể từ số thứ ba) bằng tổng của hai số liền trước. Hãy viết tiếp bốn số nữa vào dãy số.

Câu 22:

Tìm các tích bằng nhau mà không cần tính kết quả của mỗi tích.

15.2.6; 4.4.9; 5.3.12; 8.18; 15.3.4; 8.2.9

Câu 23:

Có thể tính nhẩm tích 45.6 bằng cách:

Áp dụng tính chất kết hợp của phép nhân:

45.6 = 45.(2.3) = (45.2).3 = 90 .3 = 270

Áp dụng tính chất phân phối của phép nhân đối với phép cộng:

45.6 = (40+ 5).6 = 40.6 + 5.6 = 240 +30 = 270

Hãy tính nhẩm bằng cách áp dụng tính chất kết hợp của phép nhân:

15.4; 25.12; 125.16

Câu 24:

Có thể tính nhẩm tích 45.6 bằng cách:

Áp dụng tính chất kết hợp của phép nhân:

45.6 = 45.(2.3) = (45.2).3 = 90 .3 = 270

Áp dụng tính chất phân phối của phép nhân đối với phép cộng:

45.6 = (40+ 5).6 = 40.6 + 5.6 = 240 +30 = 270

Hãy tính nhẩm bằng cách áp dụng tính chất phân phối của phép nhân đối với phép cộng:

25.12; 34.11; 47.101

Câu 25:

Áp dụng tính chất a.(b - c) = a.b – a.c để tính nhẩm. Ví dụ:

13.99 = 13.(100 - 1) = 13.100 - 13.1 = 1300 - 13 = 1287

Hãy tính: 16.19; 46.99; 35.98

Câu 26:

Sử dụng máy tính bỏ túi:

Dùng máy tính bỏ túi để tính:

375.376; 624.625; 13.81.215

Câu 27:

Đố. Số 142857 có tính chất rất đặc biệt. Hãy nhân nó với mỗi số 2, 3, 4, 5, 6 em sẽ tìm được tính chất đăc biệt ấy

Câu 28:

Bình Ngô đại cáo ra đời năm nào?

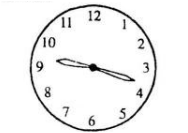
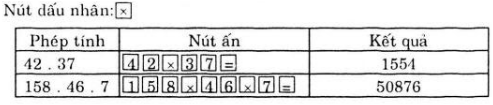
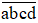Năm , Nguyễn Trãi viết Bình Ngô đại cáo tổng kết thắng lợi của cuộc kháng chiến do Lê Lợi lãnh đạo chống quân Minh. Biết rằng 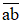là tổng số ngày trong hai tuần lễ, còn 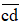gấp đôi . Tính xem năm là năm nào?

0

Đánh giá trung bình

0%

0%

0%

0%

0%

Bình luận

Bạn vui lòng để lại thông tin để được
TƯ VẤN THÊM

Hoặc gọi Hotline tư vấn: 084 283 45 85
Email: vietjackteam@gmail.com

VietJack