Đề thi Học kì 1 Toán 10 - Bộ sách Kết nối tri thức - Đề 02
40 người thi tuần này 4.0 3.6 K lượt thi 38 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
Đề kiểm tra Tích của một vecto với một số (có lời giải) - Đề 1
Đề kiểm tra Tích vô hướng của hai vectơ (có lời giải) - Đề 1
Đề kiểm tra Tổng và hiệu của hai vectơ (có lời giải) - Đề 1
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
Đề kiểm tra Bài tập cuối chương IV (có lời giải) - Đề 1
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. Có ai ở trong đó không?;
B. Bạn có thấy đói không?;
C. Đừng lại gần tôi!;
D. Số 25 không phải là số nguyên tố.
Lời giải
Đáp án đúng là: D
A. Câu trên không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.
B. Câu trên không phải là mệnh đề vì nó là câu hỏi và không khẳng định tính đúng sai.
C. Câu trên không phải là mệnh đề vì nó là câu cảm thán và không khẳng định tính đúng sai.
D. Câu này là mệnh đề vì nó khẳng định tính đúng sai.
Lời giải
Đáp án đúng là: B
Cách 1:
Ta có:
+ Các tập con có 0 phần tử: ∅.
+ Các tập con có 1 phần tử: {2}, {4}, {6}, {8}.
+ Các tập con có 2 phần tử: {2; 4}, {2; 6}, {2; 8}, {4; 6}, {4; 8}, {6; 8}.
+ Các tập con có 3 phần tử: {2; 4; 6}, {2; 4; 8}, {2; 6; 8}, {4; 6; 8}.
+ Các tập con có 4 phần tử: {2; 4; 6; 8}.
Vậy tập hợp A có 16 tập con.
Cách 2: Tập hợp A có 4 phần tử nên số tập con của tập hợp A là 24 = 16.
Câu 3
A. K = [1; 7);
B. K = (– 3; 7);
C. K = [1; 5);
D. K = [5; 7).
Lời giải
Đáp án đúng là: D
Tập hợp K là tập hợp các phần tử thuộc [1; 7) nhưng không thuộc (– 3; 5).
Ta xác định tập hợp K bằng cách vẽ trục số như sau: Trên cùng một trục số, tô đậm khoảng [1; 7) và gạch bỏ khoảng (–3; 5), sau đó bỏ luôn các khoảng chưa được tô hoặc đánh dấu. Phần tô đậm không bị gạch bỏ chính là tập hợp K.

Vậy K = [1 ; 7) \ (– 3 ; 5) = [5 ; 7).
Lời giải
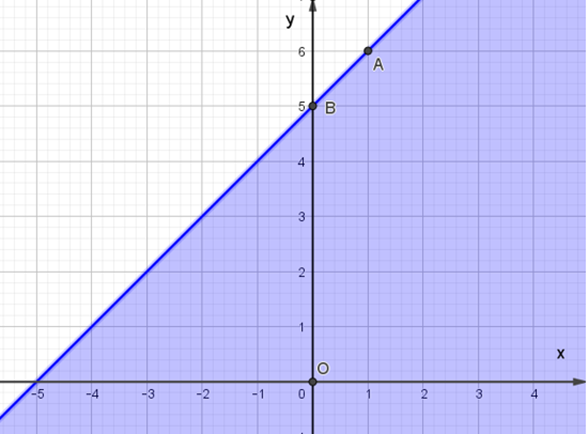
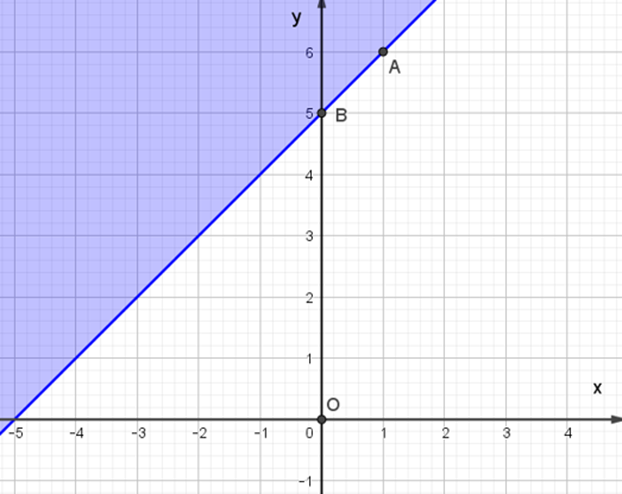
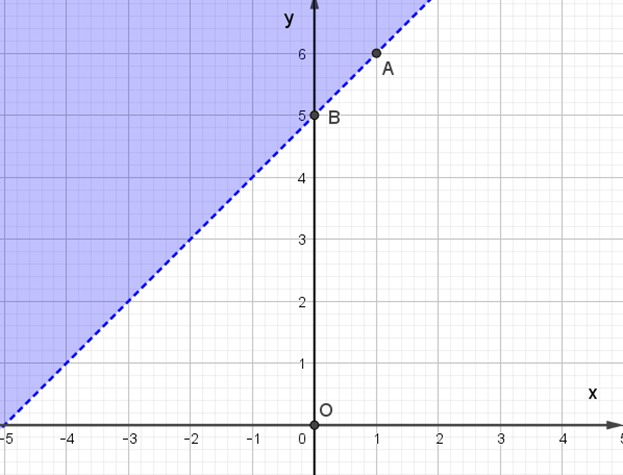
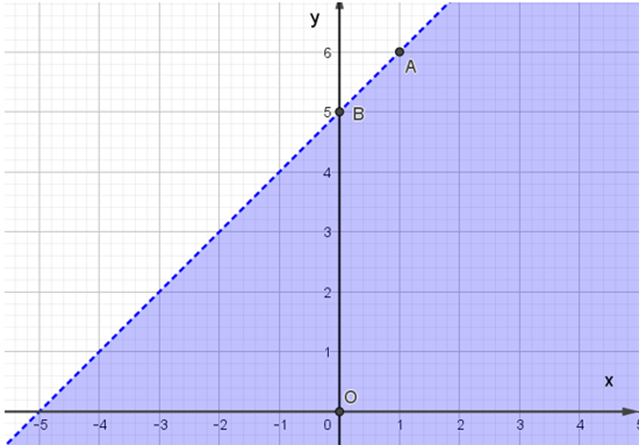
Đáp án đúng là: A
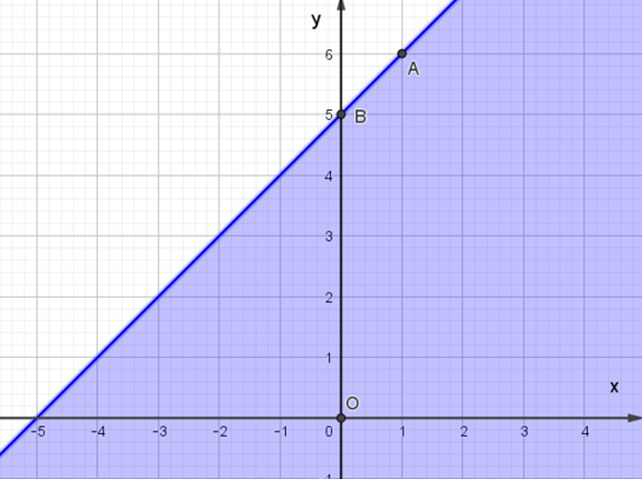
– Trên mặt phẳng Oxy vẽ đường thẳng Δ: x – y + 5 = 0 đi qua hai điểm A(1; 6) và B(0; 5).
– Xét gốc tọa độ O(0; 0). Ta thấy O không nằm trên đường thẳng Δ và 0 – 0 + 5 ≥ 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng có kể bờ Δ, chứa gốc tọa độ O (miền màu xanh trong hình ảnh).
Câu 5
A. (3; 5);
B. (1; –1);
C. (2; 5);
D. (3; 4).
Lời giải
Đáp án đúng là: B
Xét từng phương trình của hệ \(\left\{ \begin{array}{l}2x - 1 > 0\\x + 5y < 4\end{array} \right.\) hay \(\left\{ \begin{array}{l}2x - 1 > 0\\x + 5y - 4 < 0\end{array} \right.\)với cặp số (1; –1) ta có:
2.1 – 1 = 1 > 0
1 + 5.(–1) – 4 = –8 < 0
Do đó, cặp số (1; –1) là một nghiệm của hệ bất phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}2x - 1 > 0\\x + 5y < 4\end{array} \right.\) .
Câu 6
A. sin 0° = 0;
B. cos 90° = 0;
C. cos 0° = 1;
D. sin 90° = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. cos β > 0;
B. sin β > 0;
C. tan β > 0;
D. cot β > 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(\cos \alpha = \frac{2}{{13}}\);
B. \(\cos \alpha = \frac{5}{{13}}\);
C. \(\cos \alpha = - \frac{5}{{13}}\);
D. \(\cos \alpha = - \frac{2}{{13}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(2\sqrt 2 \);
B. \(2\sqrt 3 \);
C. \(2\sqrt 6 \);
D. 2\(\sqrt 5 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(\overrightarrow {AK} \) và \(\overrightarrow {KC} \) cùng phương ngược hướng;
B. \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng phương cùng hướng;
C. \(\overrightarrow {KC} \) và \(\overrightarrow {KA} \) cùng phương ngược hướng;
D. \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) cùng phương cùng hướng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. 1 cm;
B. 3 cm;
C. 4 cm;
D. 2 cm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(\overrightarrow {AB} = \overrightarrow {BC} + \overrightarrow {CA} \);
B. \(\overrightarrow {AB} = \overrightarrow {CB} + \overrightarrow {AC} \);
C. \(\overrightarrow {AB} = \overrightarrow {BC} + \overrightarrow {AC} \);
D. \(\overrightarrow {AB} = \overrightarrow {CA} + \overrightarrow {BC} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. \(\overrightarrow {AB} - \overrightarrow {AI} = \overrightarrow {BI} \);
B. \(\overrightarrow {AB} - \overrightarrow {DA} = \overrightarrow {BD} \);
C. \(\overrightarrow {AB} - \overrightarrow {DC} = \overrightarrow 0 \);
D. \(\overrightarrow {AB} - \overrightarrow {DB} = \overrightarrow 0 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Cho hình vuông ABCD cạnh 2a. Tính \(\left| {\overrightarrow {AB} - \overrightarrow {DA} } \right|\).
Cho hình vuông ABCD cạnh 2a. Tính \(\left| {\overrightarrow {AB} - \overrightarrow {DA} } \right|\).
A. \(a\sqrt 2 \);
B. a;
C. \(2a\sqrt 2 \);
D. 2a.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \);
B. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {AB} \);
C. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {AC} \);
D. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {BC} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. \[2\overrightarrow a + 3\overrightarrow b \];
B. \[ - 2\overrightarrow a + 3\overrightarrow b \];
C. \[2\overrightarrow a - 3\overrightarrow b \];
D. \[2\overrightarrow a + \overrightarrow b \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. \(\overrightarrow y \), \(\overrightarrow z \) cùng phương, ngược hướng;
B. \(\overrightarrow y \), \(\overrightarrow z \) cùng phương, cùng hướng;
C. \(\overrightarrow y \), \(\overrightarrow x \) cùng phương, ngược hướng;
D. \(\overrightarrow y \), \(\overrightarrow x \) cùng phương, cùng hướng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. I, J, C;
B. I, J, B;
C. I, A, B;
D. I, G, B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. 90°;
B. 60°;
C. 30°;
D. 45°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. 1;
B. 2;
C. \(\frac{1}{2}\);
D. \(\frac{1}{4}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. a;
B. 0;
C. a2;
D. \(\frac{1}{2}{a^2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. BD vuông góc với AC;
B. AB vuông góc với AC;
C. AB vuông góc với DC;
D. BD vuông góc với DC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. 0,003;
B. 0,03;
C. 0,0029;
D. 0,02.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. 15,3;
B. 15,31;
C. 15,32;
D. 15,4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. 9; 11; 15;
B. 2; 10,5; 15;
C. 10; 12,5; 15;
D. 9; 10,5; 15.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
A. 5;
B. 9;
C. 12;
D. 20.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
Cho mẫu số liệu sau:
15; 26; 5; 2; 9; 5; 28; 30; 2; 26.
Tính khoảng biến thiên của mẫu số liệu trên.
Cho mẫu số liệu sau:
15; 26; 5; 2; 9; 5; 28; 30; 2; 26.
Tính khoảng biến thiên của mẫu số liệu trên.
A.26;
B. 28;
C. 30;
D. 32.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. 17;
B. 18;
C. 19;
D. 20.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
A. 35,85;
B. 34,85;
C. 34,58;
D. 35,58.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
A. 7,04;
B. 8,04;
C. 7,55;
D. 8,55.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
A. 5;
B. 3;
C. \(\sqrt {13} \);
D. \(\sqrt {15} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
A. \(\overrightarrow u = \left( {3;\,\,5} \right)\);
B. \(\overrightarrow u = \left( {3;\,\, - 5} \right)\);
C. \(\overrightarrow u = \left( { - 3;\,\,5} \right)\);
D. \(\overrightarrow u = \left( { - 3;\,\, - 5} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
A. 90°;
B. 0°;
C. 135°;
D. 45°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.