Giải SBT Toán 8 Cánh Diều Hình bình hành có đáp án
32 người thi tuần này 4.6 471 lượt thi 11 câu hỏi
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
6.5 K lượt thi
15 câu hỏi
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
2.8 K lượt thi
15 câu hỏi
10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)
1.2 K lượt thi
10 câu hỏi
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
3.4 K lượt thi
10 câu hỏi
10 Bài tập Tìm giá trị đơn thức khi biết giá trị của biến (có lời giải)
669 lượt thi
10 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
13.8 K lượt thi
18 câu hỏi
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
2.1 K lượt thi
15 câu hỏi
10 Bài tập Thu gọn đơn thức (có lời giải)
697 lượt thi
10 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
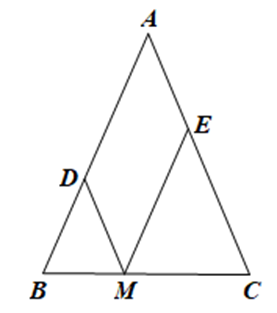
Tứ giác ADME có MD // AE, ME // AD nên ADME là hình bình hành.
Suy ra AD = ME và AE = DM.
Do đó chu vi hình bình hành ADME là:
AD + DM + ME + EA = 2(AE + ME).
Do AB = AC nên tam giác ABC cân tại A. Suy ra \(\widehat {ABC} = \widehat {ACB}\).
Mà \(\widehat {ABC} = \widehat {EMC}\) (hai góc đồng vị do ME // AB), suy ra \(\widehat {ACB} = \widehat {EMC}\).
Do đó, tam giác ECM cân tại E. Suy ra ME = CE.
Vậy chu vi của hình bình hành ADME là:
2(AE + ME) = 2(AE + CE) = 2AC = 6 cm.
Lời giải
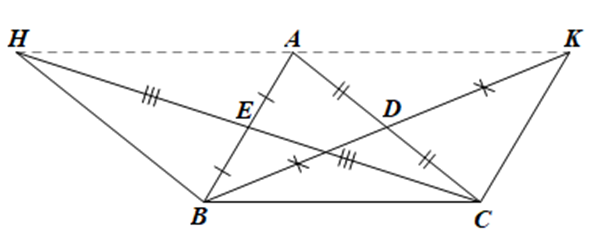
Do BD và CE là trung tuyến của ∆ABC
Suy ra, E là trung điểm AB và D là trung điểm AC.
Tứ giác AHBC có E là trung điểm AB và CH nên AHBC là hình bình hành.
Tứ giác ABCK có D là trung điểm AC và BK nên ABCK là hình bình hành.
Lời giải
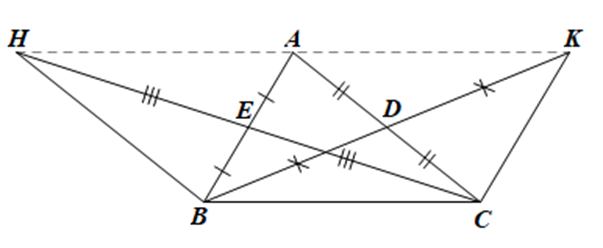
Do AHBC là hình bình hành nên AH // BC, AH = BC.
Tương tự, AKCB là hình bình hành nên AK // BC, AK = BC.
Suy ra ba điểm H, A, K thẳng hàng và AH = AK.
Vậy A là trung điểm của HK.
Lời giải
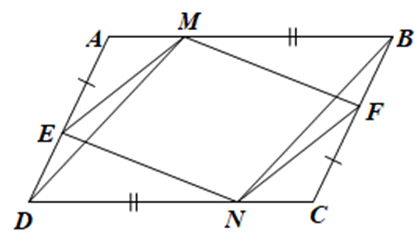
Do ABCD là hình bình hành nên AD = BC và AB = CD; \(\widehat A = \widehat C\) và \(\widehat {ABC} = \widehat {CDA}\).
Mà AE = CF, AE + ED = AD, BF + CF = BC
Suy ra DE = BF.
Tương tự, ta cũng có AM = CN.
Xét ∆AEM và ∆CFN có:
AM = CN, \(\widehat A = \widehat C\), AE = CF
Do đó ∆AEM và ∆CFN (c.g.c). Suy ra EM = FN (hai cạnh tương ứng)
Xét ∆BFM và ∆DEN có:
BF = DE, \(\widehat {ABC} = \widehat {CDA}\), BM = DN
Do đó ∆BFM = ∆DEN (c.g.c). Suy ra FM = EN.
Tứ giác EMFN có EM = FN và FM = EN nên EMFN là hình bình hành.
Lời giải
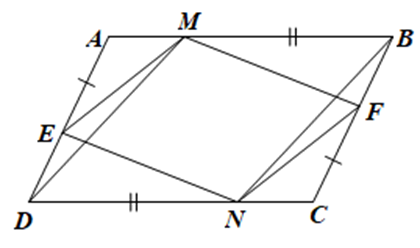
Tứ giác BMDN có BM = DN và BM // DN nên BMDN là hình bình hành.
Do ABCD, EMFN, BMDN đều là hình bình hành nên các đường chéo của mỗi hình bình hành cắt nhau tại trung điểm của mỗi đường.
Vậy AC, BD, EF, MN cùng đi qua trung điểm của mỗi đường.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo