Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 10
21 người thi tuần này 4.6 2.4 K lượt thi 4 câu hỏi 45 phút
🔥 Đề thi HOT:
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
20 câu trắc nghiệm Toán 8 Kết nối tri thức Ôn tập chương I (Đúng sai - trả lời ngắn) có đáp án
Trắc nghiệm Bài tập cơ bản Những hằng đẳng thức đáng nhớ có đáp án
3 câu Trắc nghiệm Toán 8 Bài 12: Hình vuông có đáp án (Vận dụng)
2 câu Trắc nghiệm Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước có đáp án (Vận dụng cao)
6 câu Trắc nghiệm Toán 8 Bài 11: Hình thoi có đáp án (Vận dụng)
10 câu Trắc nghiệm Toán 8 Bài 4: Phương trình tích có đáp án (Vận dụng)
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
1. Biểu đồ đoạn thẳng biểu diễn vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của Việt Nam qua các năm 2015; 2017; 2018; 2019; 2020. (đơn vị: nghìn tỷ đồng)
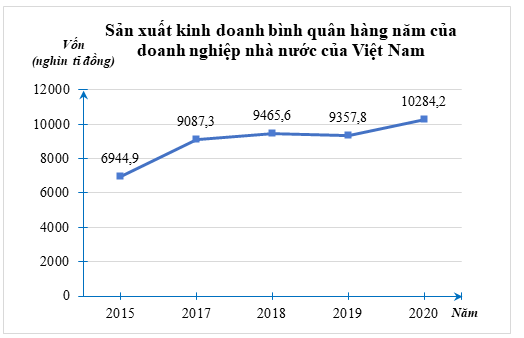
(Nguồn: Niên giám thống kê 2021)
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng bao nhiêu phần trăm so năm 2015 (làm tròn kết quả đến hàng phần mười)?
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng bao nhiêu phần trăm so năm 2015 (làm tròn kết quả đến hàng phần mười)?
c) Tính tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong năm 2020 và tổng số vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong các năm còn lại (làm tròn kết quả đến hàng phần mười).
2. Một túi đựng bút tô màu của bé Mai có 5 chiếc bút màu vàng, 3 chiếc bút màu cam, 4 chiếc bút màu xanh và 2 chiếc bút màu tím (các chiếc bút có cùng khối lượng và kích thước). Bé Mai lấy ngẫu nhiên một chiếc bút từ trong túi.
a) Hỏi có bao nhiêu kết quả đồng khả năng?
b) Tính xác suất của biến cố E: “Lấy được chiếc bút màu tím”;
c) Tính xác suất của biến cố F: “Lấy được chiếc bút màu cam hoặc màu xanh”.
1. Biểu đồ đoạn thẳng biểu diễn vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của Việt Nam qua các năm 2015; 2017; 2018; 2019; 2020. (đơn vị: nghìn tỷ đồng)

(Nguồn: Niên giám thống kê 2021)
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng bao nhiêu phần trăm so năm 2015 (làm tròn kết quả đến hàng phần mười)?
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng bao nhiêu phần trăm so năm 2015 (làm tròn kết quả đến hàng phần mười)?
c) Tính tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong năm 2020 và tổng số vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong các năm còn lại (làm tròn kết quả đến hàng phần mười).
2. Một túi đựng bút tô màu của bé Mai có 5 chiếc bút màu vàng, 3 chiếc bút màu cam, 4 chiếc bút màu xanh và 2 chiếc bút màu tím (các chiếc bút có cùng khối lượng và kích thước). Bé Mai lấy ngẫu nhiên một chiếc bút từ trong túi.
a) Hỏi có bao nhiêu kết quả đồng khả năng?
b) Tính xác suất của biến cố E: “Lấy được chiếc bút màu tím”;
c) Tính xác suất của biến cố F: “Lấy được chiếc bút màu cam hoặc màu xanh”.
Lời giải
1. a) Biểu đồ đã cho là biểu đồ đoạn thẳng.
Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập gián tiếp bằng cách truy cập website của Niên giám thống kê 2021.
b) Tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước năm 2020 so với năm 2015 là: \(\frac{{10\,\,284,2}}{{6\,\,944,9}} \cdot 100\% \approx 148,1\% \).
Vậy năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng khoảng \[148,1\% - 100\% = 48,1\% \] so năm 2015.
c) Tổng tổng số vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong các năm 2015; 1017; 2018; 2019 là:
\[6\,\,944,9 + 9\,\,087,3 + 9\,\,465,6 + 9\,\,357,8 = 3\,\,4855,6\] (nghìn tỉ đồng).
Tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong năm 2020 và tổng số vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong các năm còn lại (các năm 2015; 1017; 2018; 2019) là:
\(\frac{{1\,\,0284,2}}{{3\,\,4855,6}} \cdot 100\% \approx 0,3\% \).
Vậy tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong năm 2020 và tổng số vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước trong các năm còn lại khoảng \(0,3\% \).
2. a) Có \(5 + 3 + 4 + 2 = 14\) kết quả có thể xảy ra và các kết quả là đồng khả năng.
Vậy có 14 kết quả là đồng khả năng.
b) Xác suất của biến cố E là \(P\left( E \right) = \frac{2}{{14}} = \frac{1}{7}.\)
c) Số kết quả thuận lợi lấy được chiếc bút màu cam hoặc màu xanh là: \(3 + 4 = 7.\)
Xác suất của biến cố F là \(P\left( F \right) = \frac{7}{{14}} = \frac{1}{2}.\)
Lời giải
|
\[4x--2x = 5 + 1\] \[2x = 6\] \[x = 3\] Vậy nghiệm của phương trình là \[x = 3\]. |
b) \(\frac{{x - 2}}{6} - \frac{x}{2} = \frac{{5 - 2x}}{3}\) \(\frac{{x - 2}}{6} - \frac{{3x}}{6} = \frac{{2\left( {5 - 2x} \right)}}{6}\) \(x - 2 - 3x = 2\left( {5 - 2x} \right)\) \( - 2x - 2 = 10 - 4x\) \(2x = 12\). \(x = 6\) Vậy nghiệm của phương trình là \(x = 6.\) |
2. Gọi số tuổi hiện nay của người thứ nhất là x (tuổi), x nguyên, dương.
Số tuổi người thứ nhất cách đây 10 năm là: \[x - 10\] (tuổi).
Số tuổi người thứ hai cách đây 10 năm là: \(\frac{{x - 10}}{3}\) (tuổi).
Sau đây 2 năm tuổi người thứ nhất là: \[x + 2\] (tuổi).
Sau đây 2 năm tuổi người thứ hai là: \(\frac{{x + 2}}{2}\) (tuổi).
Theo bài ra ta có phương trình phương trình như sau:
\(\frac{{x + 2}}{2} = \frac{{x - 10}}{3} + 10 + 2\)
\(\frac{{x + 2}}{2} - \frac{{x - 10}}{3} = 12\)
\(\frac{{3\left( {x + 2} \right)}}{6} - \frac{{2\left( {x - 10} \right)}}{6} = \frac{{72}}{6}\)
\(3\left( {x + 2} \right) - 2\left( {x - 10} \right) = 72\)
\(3x + 6 - 2x + 20 = 72\)
\(3x + 6 - 2x + 20 = 72\)
\[x = 46\] (TMĐK).
Khi đó, số tuổi hiện nay của người thứ hai là: \(\frac{{46 + 2}}{2} - 2 = 12\) (tuổi).
Lời giải
1. Ta có \(AB \bot AE;\,\,CD \bot AE\) nên \(CD\,{\rm{//}}\,AB\).
Xét tam giác \(ABE\) có \(CD\,{\rm{//}}\,AB\), ta có
\[\,\frac{{DE}}{{AB}} = \frac{{EC}}{{EA}}\] (hệ quả của định lí Thalès).
Hay \[\frac{{1,5}}{{AB}} = \frac{2}{{2 + 8}}\] suy ra \[AB = 7,5\,\,{\rm{m}}\].
Vậy chiều cao của cây là \[7,5\,\,{\rm{m}}\].
2.
![1. Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao \[1,5\,\,{\rm{m}}\] so với mặt đất, chân cọc cách gốc cây \[8\,\,{\rm{m}}\] và cách bóng của đỉnh cọc \[2\,\,{\rm{m}}.\] Tính chiều cao của cây (kết quả làm tròn đến chữ số thập phân thứ nhất). 2. Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right).\] Kẻ đường cao \[BE,{\rm{ }}AK\] và \[CF\] cắt nhau tại \[H.\] a) Chứng minh: . b) Chứng minh: \(AE \cdot AC = AF \cdot AB\). c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid10-1751278297.png)
a) Xét \[\Delta ABK\] và \[\Delta CBF\] có:
\[\widehat {ABK} = \widehat {CBF}\;\left( {\widehat B\;\,{\rm{chung}}} \right)\]; \(\widehat {AKB} = \widehat {CFB}\;\left( { = 90^\circ } \right)\)
Do đó .
b) Xét \[\Delta AEB\] và \[\Delta ACF\] có:
\(\widehat {EAB} = \widehat {FAC}\;\,\left( {\widehat A\;\,{\rm{chung}}} \right)\); \(\widehat {AEB} = \widehat {AFC}\;\left( { = 90^\circ } \right)\)
Do đó
Suy ra \(\frac{{AE}}{{AF}} = \frac{{AB}}{{AC}}\) hay \(AE \cdot AC = AF \cdot AB\) (đpcm)
c) Xét \[\Delta BFC\] vuông tại \[F\] có \[O\] là trung điểm của \[BC\] nên \(FO = \frac{{BC}}{2}\).
Xét \[\Delta BEC\] vuông tại \[E\] có \[O\] là trung điểm của \[BC\] nên \(EO = \frac{{BC}}{2}\).
Do đó \[FO = EO = \frac{{BC}}{2}\]. (1)
Xét \[\Delta AEH\] vuông tại \[E\] có \[I\] là trung điểm của \[AH\] nên \(EI = \frac{{AH}}{2}\).
Xét \[\Delta AFH\] vuông tại \[F\] có \[I\] là trung điểm của \[AH\] nên \(FI = \frac{{AH}}{2}\).
Do đó \[FI = EI = \frac{{AH}}{2}\]. (2)
Từ (1) và (2) ta suy ra được \[OI\] là đường trung trực của cạnh \[EF\].
Khi đó \[OI \bot EF\] hay \[OI \bot DN\].
Do đó \[DN\] là đường cao của \[\Delta DOI\].
Xét \[\Delta DOI\] có \[DN\] và \[IK\] là đường cao và \[N\] là giao của \[DN\] và \[IK\].
Do đó \[N\] là trực tâm của tam giác \[DOI\].
Vậy \[OI \bot DI\] (đpcm).
Lời giải
Các trường hợp có thể xảy ra khi chọn hai tấm thẻ bất kì là:
\[\left\{ { - 2\,;\,\, - 1} \right\}\,;\,\,\left\{ { - 2\,;\,\,0} \right\}\,;\,\,\left\{ { - 2\,;\,\,3} \right\}\,;\,\,\left\{ { - 2\,;\,\,4} \right\};\left\{ { - 2;5} \right\}\];
\[\left\{ { - 1\,;\,\,0} \right\}\,;\,\,\left\{ { - 1\,;\,\,3} \right\}\,;\,\,\left\{ { - 1\,;\,\,4} \right\}\,;\,\,\left\{ { - 1\,;\,\,5} \right\}\];
\[\left\{ {0\,;\,\,3} \right\};\left\{ {0\,;\,\,4} \right\}\,;\,\,\left\{ {0\,;\,\,5} \right\}\]; \[\left\{ {3\,;\,\,4} \right\}\,;\,\,\left\{ {3\,;\,\,5} \right\}\,;\,\,\left\{ {4;5} \right\}\].
Và ngược lại đổi vị trí hai số trong các cặp số trên.
Số các kết quả xảy ra khi chọn hai tấm thẻ phân biệt từ tập hợp đã cho là \[15 \cdot 2 = 30\].
Khi tích của hai số đã chọn bằng 0 thì số hạng đầu tiên bằng 0 hoặc số hạng thứ 2 bằng 0, ta có 10 trường hợp như thế.
Vậy xác xuất cần tìm là \[\frac{{10}}{{30}} = \frac{1}{3}\].
![1. Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao \[1,5\,\,{\rm{m}}\] so với mặt đất, chân cọc cách gốc cây \[8\,\,{\rm{m}}\] và cách bóng của đỉnh cọc \[2\,\,{\rm{m}}.\] Tính chiều cao của cây (kết quả làm tròn đến chữ số thập phân thứ nhất). 2. Cho tam giác \[ABC\] có ba góc nhọn \[\left( {AB < AC} \right).\] Kẻ đường cao \[BE,{\rm{ }}AK\] và \[CF\] cắt nhau tại \[H.\] a) Chứng minh: . b) Chứng minh: \(AE \cdot AC = AF \cdot AB\). c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid11-1751278322.png)