Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 9
21 người thi tuần này 4.6 2.4 K lượt thi 4 câu hỏi 45 phút
🔥 Đề thi HOT:
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
20 câu trắc nghiệm Toán 8 Kết nối tri thức Ôn tập chương I (Đúng sai - trả lời ngắn) có đáp án
Trắc nghiệm Bài tập cơ bản Những hằng đẳng thức đáng nhớ có đáp án
3 câu Trắc nghiệm Toán 8 Bài 12: Hình vuông có đáp án (Vận dụng)
2 câu Trắc nghiệm Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước có đáp án (Vận dụng cao)
6 câu Trắc nghiệm Toán 8 Bài 11: Hình thoi có đáp án (Vận dụng)
10 câu Trắc nghiệm Toán 8 Bài 4: Phương trình tích có đáp án (Vận dụng)
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
1. Biểu đồ cột biểu diễn sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020 (đơn vị: nghìn tấn):
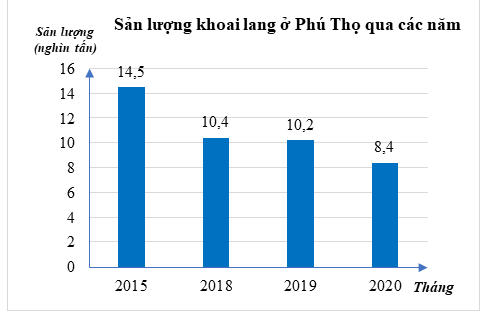
(Nguồn: Niên giám thống kê 2021)
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Năm 2019 sản lượng khoai lang ở Phú Thọ tăng hay giảm bao nhiêu phần trăm so với năm 2015 (làm tròn kết quả đến hàng phần mười)? Em có nhận xét gì về sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020.
c) Một bài báo đã nêu nhận định sau: “Năm 2020 sản lượng khoai lang ở Phú Thọ là ít nhất, năm 2020 sản lượng khoai lang ở Phú Thọ giảm \[19,2\% \] so với năm 2018”. Theo em, nhận định của bài báo đó có chính xác không?
2. Phúc gieo một con xúc xắc 50 lần và thống kê lại kết quả các lần gieo ở bảng sau:
Mặt
1 chấm
2 chấm
3 chấm
4 chấm
5 chấm
6 chấm
Số lần xuất hiện
8
9
9
5
6
13
a) Hỏi số lần gieo được mặt có số chấm là số chẵn là bao nhiêu?
b) Tính xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm là số lẻ”.
c) Tính xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm nhỏ hơn 3 chấm”.
1. Biểu đồ cột biểu diễn sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020 (đơn vị: nghìn tấn):

(Nguồn: Niên giám thống kê 2021)
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Năm 2019 sản lượng khoai lang ở Phú Thọ tăng hay giảm bao nhiêu phần trăm so với năm 2015 (làm tròn kết quả đến hàng phần mười)? Em có nhận xét gì về sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020.
c) Một bài báo đã nêu nhận định sau: “Năm 2020 sản lượng khoai lang ở Phú Thọ là ít nhất, năm 2020 sản lượng khoai lang ở Phú Thọ giảm \[19,2\% \] so với năm 2018”. Theo em, nhận định của bài báo đó có chính xác không?
2. Phúc gieo một con xúc xắc 50 lần và thống kê lại kết quả các lần gieo ở bảng sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
8 |
9 |
9 |
5 |
6 |
13 |
a) Hỏi số lần gieo được mặt có số chấm là số chẵn là bao nhiêu?
b) Tính xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm là số lẻ”.
c) Tính xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm nhỏ hơn 3 chấm”.
Lời giải
1. a) Biểu đồ đã cho là biểu đồ cột.
Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập gián tiếp bằng cách truy cập website của Niên giám thống kê 2021.
b) Ta thấy sản lượng khoai lang Phú Thọ năm 2019 nhỏ hơn sản lượng khoai lang Phú Thọ năm 2015 (vì \(10,2 < 14,5\)).
Do đó, sản lượng khoai lang Phú Thọ năm 2019 giảm so với năm 2015.
Tỉ số phần trăm sản lượng khoai lang ở Phú Thọ trong năm 2019 so với năm 2015 là:
\(\frac{{10,2}}{{14,5}} \cdot 100\% \approx 70,3\% \).
Vậy năm 2019 sản lượng khoai lang ở Phú Thọ tăng khoảng \(100\% - 70,3\% = 29,7\% \) so với năm 2015.
c) Năm 2020 sản lượng khoai lang ở Phú Thọ là 8,4 nghìn tấn ít nhất so với các năm còn lại.
Tỉ số phần trăm sản lượng khoai lang ở Phú Thọ năm 2020 so với năm 2018 là:
\(\frac{{8,4}}{{10,4}} = 80,8\% \).
Năm 2020 sản lượng khoai lang ở Phú Thọ giảm \[19,2\% \] so với năm 2018.
Theo em nhận định của bài báo đó chính xác.
2. a) Trong 50 lần thử, số lần gieo được mặt có số chấm là số chẵn là:
\[9 + 5 + 13 = 27\] (lần).
Vậy số lần gieo được mặt có số chấm là số chẵn là 27.
b) Trong 50 lần thử, số lần gieo được mặt có số chấm là số lẻ là:
\[50 - 27 = 23\] (lần).
Xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm là số lẻ” sau 50 lần thử trên là \[\frac{{23}}{{50}} = 0,46\].
c) Trong 50 lần thử, số lần gieo được mặt có số chấm nhỏ hơn 3 chấm là:
\[8 + 9 + 9 = 26\] (lần).
Xác suất thực nghiệm của biến cố “Gieo được mặt có số chấm nhỏ hơn 3 chấm” sau 50 lần thử trên là \[\frac{{26}}{{50}} = 0,52\].
Lời giải
|
\[6x--3x = --2--7\] \[3x = --9\] \[x = --3\] Vậy nghiệm của phương trình là \[x = --3\]. |
b) \(\frac{{2x - 1}}{3} + \frac{{x + 4}}{2} = \frac{{5x + 20}}{6}\) \[\frac{{2\left( {2x - 1} \right)}}{6} + \frac{{3\left( {x + 4} \right)}}{6} = \frac{{5x + 20}}{6}\] \[\frac{{4x - 2}}{6} + \frac{{3x + 12}}{6} = \frac{{5x + 20}}{6}\] \[\frac{{7x + 10}}{6} = \frac{{5x + 20}}{6}\] \[7x + 10 = 5x + 20\] \[7x - 5x = 20 - 10\] \[2x = 10\] \[x = 5\] Vậy nghiệm của phương trình là \[x = 5.\] |
2. Gọi x (kg) là khối lượng của chất lỏng thứ hai \(\left( {x > 0} \right).\)
Khối lượng của chất lỏng thứ nhất là \(x + 2\,\,\left( {{\rm{kg}}} \right){\rm{.}}\)
Thể tích của chất lỏng thứ nhất là
Thể tích của chất lỏng thứ hai là
Thể tích của hỗn hợp chất lỏng là
Theo đề bài, ta có phương trình:
\(\frac{{x + 2}}{{700}} + \frac{x}{{500}} = \frac{{2x + 2}}{{600}}\)
\(\frac{{x + 2}}{7} + \frac{x}{5} = \frac{{2x + 2}}{6}\)
\(30\left( {x + 2} \right) + 42x = 35\left( {2x + 2} \right)\)
\(30x + 60 + 42x = 70x + 70\)
\(2x = 10\)
\(x = 5\) (nhận)
Vậy khối lượng của chất lỏng thứ hai là 5 kg.Lời giải
1.
![1. Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như hình vẽ bên) sao cho hai chân thang rộng một khoảng là 80 cm. Hỏi người thợ đã làm thanh ngang đó dài bao nhiêu cm? 2. Cho tam giác \[ABC\] vuông tại \[A,\] đường cao \[AH,\] biết \[AB = 6\,\,{\rm{cm;}}\].\[AC = 8\,\,{\rm{cm}}.\]. a) Chứng minh: \[\Delta ABC\] đồng dạng \[\Delta HBA.\] Tính \[HB\,,{\rm{ }}AH.\] b) Lấy điểm \[M\] trên cạnh \[AC\] (\[M\] khác \[A\] và \[C\]), kẻ \[CI\] vuông góc với \[BM\] tại \[I.\]Chứng minh: \[MA \cdot MC = MB \cdot MI.\] c) Xác định vị trí điểm \[M\] thuộc cạnh \[AC\] để diện tích tam giác \[BIC\] đạt giá trị lớn nhất. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid7-1751277699.png)
Gọi \[MN\] là thanh ngang; \[BC\] là độ rộng giữa hai bên thang.
Thanh ngang \[MN\] nằm chính giữa thang nên \[M;{\rm{ }}N\]là trung điểm \[AB\] và \[AC.\]
Suy ra \[MN\] là đường trung bình của tam giác \[ABC.\]
Suy ra \(MN = \frac{1}{2}BC = \frac{1}{2}.80 = 40\,\,{\rm{(cm)}}\).
Vậy người thợ đã làm thanh ngang đó dài \[40{\rm{ cm}}.\]
2.
![1. Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như hình vẽ bên) sao cho hai chân thang rộng một khoảng là 80 cm. Hỏi người thợ đã làm thanh ngang đó dài bao nhiêu cm? 2. Cho tam giác \[ABC\] vuông tại \[A,\] đường cao \[AH,\] biết \[AB = 6\,\,{\rm{cm;}}\].\[AC = 8\,\,{\rm{cm}}.\]. a) Chứng minh: \[\Delta ABC\] đồng dạng \[\Delta HBA.\] Tính \[HB\,,{\rm{ }}AH.\] b) Lấy điểm \[M\] trên cạnh \[AC\] (\[M\] khác \[A\] và \[C\]), kẻ \[CI\] vuông góc với \[BM\] tại \[I.\]Chứng minh: \[MA \cdot MC = MB \cdot MI.\] c) Xác định vị trí điểm \[M\] thuộc cạnh \[AC\] để diện tích tam giác \[BIC\] đạt giá trị lớn nhất. (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid8-1751277717.png)
a) Áp dụng định lý Pythagore vào tam giác \[ABC\] vuông tại \[A,\] ta có: \(A{B^2} + A{C^2} = B{C^2}\)
Suy ra \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + {8^2}} = 10\;\,{\rm{(cm)}}\).
Xét hai tam giác \[ABC\] và \[HBA\] có
\(\widehat {AHB} = \widehat {CAB}\;\left( { = 90^\circ } \right)\); \(\widehat {HBA} = \widehat {ABC}\,\;\left( {\widehat B\;\,{\rm{chung}}} \right)\)
Do đó .
Áp dụng định lý Pythagore vào tam giác \[ABH\] vuông tại \[H\] có
\(A{B^2} = B{H^2} + A{H^2}\)
Suy ra \(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{6^2} - {{3,6}^2}} = 4,8\;\,{\rm{(cm)}}\).
Vậy \[HB = 3,6{\rm{ cm}};{\rm{ }}AH = 4,8{\rm{ cm}}.\]
b) Xét \(\Delta MAB\) và \(\Delta MIC\) có:
\(\widehat {MAB} = \widehat {MIC}\;\left( { = 90^\circ } \right)\); \(\widehat {AMB} = \widehat {IMC}\).
Do đó .
Suy ra .
Khi đó \(\frac{{MA}}{{MI}} = \frac{{MB}}{{MC}}\) hay \(MA \cdot MC = MB \cdot MI\) (đpcm).
c) Diện tích tam giác \(BIC\) là: \({S_{BIC}} = \frac{1}{2}IB \cdot IC\). (1)
Ta có: \[{\left( {IB - {\rm{ }}IC} \right)^2} \ge 0\]
\[I{B^2} + {\rm{ }}I{C^2} - 2IB \cdot IC \ge 0\]
\[I{B^2} + {\rm{ }}I{C^2} \ge 2IB \cdot IC\]
\(IB.IC \le \frac{{I{B^2} + I{C^2}}}{2}\).
Mặt khác, áp dụng định lý Pythagore vào tam giác \(BIC\) vuông tại \[I\] nên
\[B{C^2} = I{B^2} + I{C^2}\]
Thay vào (1) ta suy ra được:
\({S_{BIC}} \le \frac{1}{2} \cdot \frac{{I{B^2} + I{C^2}}}{2} = \frac{{B{C^2}}}{4} = \frac{{10}}{4} = \frac{5}{2}\;\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Dấu xảy ra khi và chỉ khi \[IB = IC.\]
Suy ra \(\Delta IBC\) cân tại \[I\] nên tam giác \(IBC\) vuông cân tại \[I\], suy ra \(\widehat {MBC} = 45^\circ .\)
Vậy khi điểm \[M\] thuộc \[AC\] sao cho \(\widehat {MBC} = 45^\circ \) thì diện tích tam giác \(BIC\) đạt giá trị lớn nhất.
Lời giải
Gọi số ghi trên thẻ rút được từ hộp 1 là \(a,\) từ hộp 2 là \(b,\) từ hộp 3 là \(c.\)
Với \(a \in \left\{ {1\,;\,\,2\,;\,\,3} \right\}, & b \in \left\{ {2\,;\,\,4\,;\,\,6\,;\,\,8} \right\}, & c \in \left\{ {1\,;\,\,3\,;\,\,5\,;\,\,7\,;\,\,9\,;\,\,11} \right\}.\)
Khi đó, số các kết quả có thể rút được ba thẻ là \(\left( {a\,;\,\,b\,;\,\,c} \right)\) là \(3 \cdot 4 \cdot 6 = 72\) (cách).
Và các kết quả có thể xảy ra này là đồng khả năng.
Gọi \(A\) là biến cố rút được ba thẻ ghi số \(a\,,\,\,b\,,\,\,c\) và \(a + b + c\) là số lẻ.
Vì \(b \in \left\{ {2\,;\,\,4\,;\,\,6\,;\,\,8} \right\},\,\,\,c \in \left\{ {1\,;\,\,3\,;\,\,5\,;\,\,7\,;\,\,9\,;\,\,11} \right\}\) nên \(b + c\) là số lẻ.
Để \(a + b + c\) là số lẻ và \(a \in \left\{ {1\,;\,\,2\,;\,\,3} \right\}\) thì
Do đó, số kết quả thuận lợi để biến cố \(A\) xảy ra là: \(1 \cdot 4 \cdot 6 = 24\).
Vậy xác suất để biến cố \(A\) xảy ra là \(P\left( A \right) = \frac{{24}}{{72}} = \frac{1}{3}.\)
![1. Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như hình vẽ bên) sao cho hai chân thang rộng một khoảng là 80 cm. Hỏi người thợ đã làm thanh ngang đó dài bao nhiêu cm? 2. Cho tam giác \[ABC\] vuông tại \[A,\] đường cao \[AH,\] biết \[AB = 6\,\,{\rm{cm;}}\].\[AC = 8\,\,{\rm{cm}}.\]. a) Chứng minh: \[\Delta ABC\] đồng dạng \[\Delta HBA.\] Tính \[HB\,,{\rm{ }}AH.\] b) Lấy điểm \[M\] trên cạnh \[AC\] (\[M\] khác \[A\] và \[C\]), kẻ \[CI\] vuông góc với \[BM\] tại \[I.\]Chứng minh: \[MA \cdot MC = MB \cdot MI.\] c) Xác định vị trí điểm \[M\] thuộc cạnh \[AC\] để diện tích tam giác \[BIC\] đạt giá trị lớn nhất. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/06/blobid9-1751277940.png)