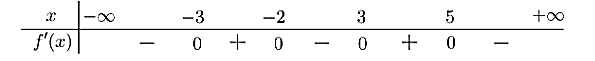Đề thi giữa kì 1 Toán 12 Kết Nối Tri Thức có đáp án - Đề 09
33 người thi tuần này 4.6 3.3 K lượt thi 38 câu hỏi 90 phút
🔥 Đề thi HOT:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải (P1)
240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1)
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: D
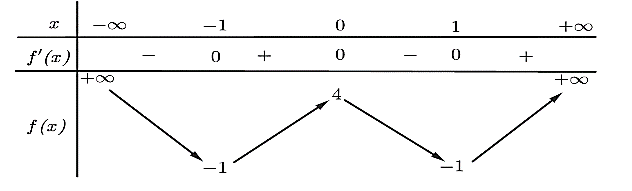
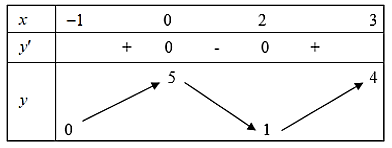
Dựa vào bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
Lời giải
Đáp án đúng là: D
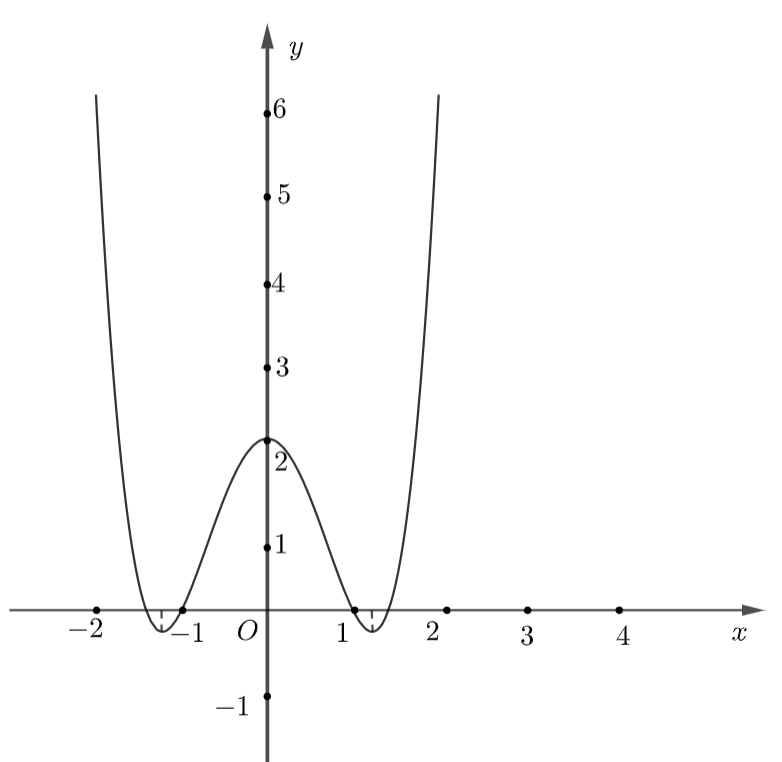
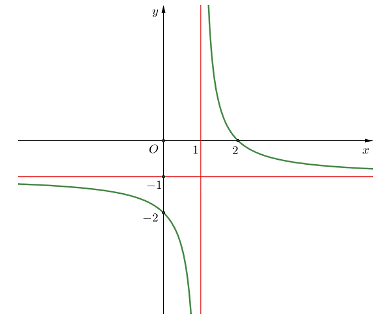
Quan sát đồ thị hàm số, ta có:
Trên khoảng \(\left( {0;1} \right)\), đồ thị hàm số đi xuống từ trái sang phải nên hàm số đã cho nghịch biến trên khoảng này.
Vậy hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\).
Lời giải
Đáp án đúng là: D
Quan sát bảng xét dấu, ta thấy hàm số có 4 điểm cực trị.
Lời giải
Đáp án đúng là: B
Ta có: \[y = {x^3}--3{x^2} + 2\] \( \Rightarrow \) \(y' = 3{x^2} - 6x\).
\(y' = 0\)\( \Leftrightarrow \)\(3{x^2} - 6x = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 0\end{array} \right.\).
Ta có bảng biến thiên như sau:
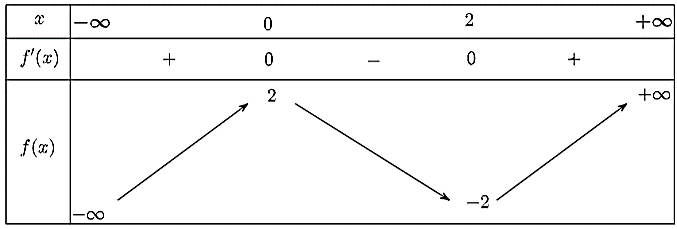
Vậy hàm số đạt cực tiểu tại \(x = 2\) và đạt cực đại tại \(x = 0\).
Lời giải
Đáp án đúng là: B
Ta có: \(y = 3{x^4} - 6{x^2} + 1\) \( \Rightarrow y' = 12{x^3} - 12x\).
\(y' = 0 \Leftrightarrow 12{x^3} - 12x = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1.\end{array} \right.\)
Ta có bảng biến thiên như sau:
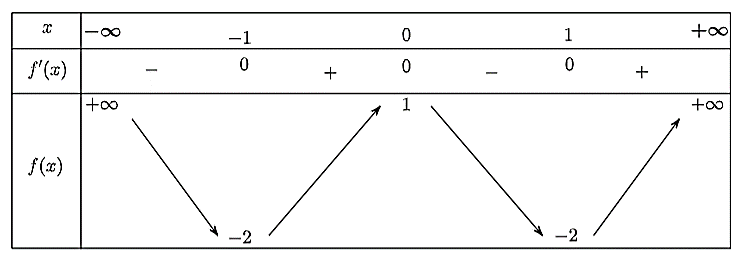
Quan sát bảng biến thiên, ta thấy:
Hàm số đạt cực đại tại \(x = 0\) và
Hàm số đạt cực tiểu tại \(x = \pm 1\) và \({y_{CT}} = - 2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.