Bộ 5 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án - Đề 3
23 người thi tuần này 4.6 4.4 K lượt thi 22 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Câu 1
A. Số huy chương vàng mà các vận động viên đã đạt được.
B. Danh sách các vận động viên tham dự Omlypic Tokyo 2020: Nguyễn Huy Hoàng, Nguyễn Thị Ánh Viên,…
C. Số học sinh nữ của các tổ trong lớp 8A.
Lời giải
Đáp án đúng là: B
Trong các dữ liệu đã cho, dữ liệu định tính là danh sách các vận động viên tham dự Omlypic Tokyo 2020: Nguyễn Huy Hoàng, Nguyễn Thị Ánh Viên,…
Câu 2
A. Dữ liệu số rời rạc.
B. Dữ liệu số liên tục.
Lời giải
Đáp án đúng là: A
Dữ liệu về số người trong mỗi gia đình ở xóm em là dữ liệu số dời dạc.
Câu 3
Lời giải
Đáp án đúng là: B
Để thu thập dữ liệu trên, bạn An đứng ở cổng trường và quan sát rồi ghi lại xem bạn nào ra về bằng xe đạp khi tan trường.
Do đó, phương pháp bạn An thu được dữ liệu là quan sát.
Câu 4
Nhiệt độ trung bình các tháng trong năm của một quốc gia được biểu diễn như sau:
|
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Nhiệt độ (độ C) |
2 |
3 |
5 |
15 |
20 |
30 |
29 |
27 |
20 |
15 |
12 |
7 |
Biểu đồ thích hợp để biểu diễn dữ liệu trong bảng trên là
A. Biểu đồ hình quạt tròn.
B. Biểu đồ cột tranh.
Lời giải
Đáp án đúng là: C
Biểu đồ thích hợp để biểu diễn dữ liệu trong bảng trên là biểu đồ đoạn thẳng.
Câu 5
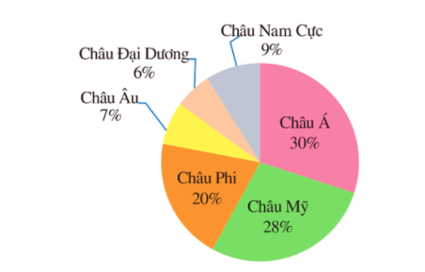
A. \(20\% .\)
Lời giải
Đáp án đúng là: C
Dựa vào biểu đồ, ta thấy châu Mỹ chiếm \(28\% \) tổng diện tích của cả sáu châu lục đó.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
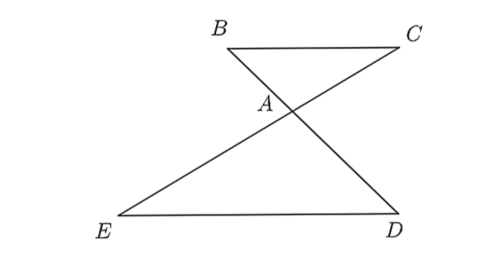
A. \(\frac{{AB}}{{AD}} = \frac{{BC}}{{DE}}.\)
B. \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Cho \(\Delta ABC\) có \(D,E\) lần lượt là hai điểm nằm trên \(AB\) và \(BC\) sao cho \(\frac{{AD}}{{AB}} = \frac{{CE}}{{CB}}\). Cho các khẳng định sau:
(I). \(DE\) là đường trung bình của \(\Delta ABC\).
(II). \(DE\parallel AC\).
(III). \(\frac{{DB}}{{BA}} = \frac{{DE}}{{AC}} = \frac{1}{2}\).
Khẳng định nào dưới đây là đúng?
Cho \(\Delta ABC\) có \(D,E\) lần lượt là hai điểm nằm trên \(AB\) và \(BC\) sao cho \(\frac{{AD}}{{AB}} = \frac{{CE}}{{CB}}\). Cho các khẳng định sau:
(I). \(DE\) là đường trung bình của \(\Delta ABC\).
(II). \(DE\parallel AC\).
(III). \(\frac{{DB}}{{BA}} = \frac{{DE}}{{AC}} = \frac{1}{2}\).
Khẳng định nào dưới đây là đúng?
A. Chỉ có (I) đúng.
B. Chỉ có (II) đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Cho \(\Delta ABC\) có \(D,E\) lần lượt là hai điểm nằm trên \(AB\) và \(BC\) sao cho \(\frac{{AD}}{{AB}} = \frac{{CE}}{{CB}}\). Cho các khẳng định sau:
(I). \(DE\) là đường trung bình của \(\Delta ABC\).
(II). \(DE\parallel AC\).
(III). \(\frac{{DB}}{{BA}} = \frac{{DE}}{{AC}} = \frac{1}{2}\).
Khẳng định nào dưới đây là đúng?
Cho \(\Delta ABC\) có \(D,E\) lần lượt là hai điểm nằm trên \(AB\) và \(BC\) sao cho \(\frac{{AD}}{{AB}} = \frac{{CE}}{{CB}}\). Cho các khẳng định sau:
(I). \(DE\) là đường trung bình của \(\Delta ABC\).
(II). \(DE\parallel AC\).
(III). \(\frac{{DB}}{{BA}} = \frac{{DE}}{{AC}} = \frac{1}{2}\).
Khẳng định nào dưới đây là đúng?
A. Chỉ có (I) đúng.
B. Chỉ có (II) đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. Đường trung bình của tam giác là đường nối hai cạnh của tam giác.
B. Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.
C. Trong một tam giác chỉ có một đường trung bình.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.