Đường thẳng đi qua hai điểm
57 người thi tuần này 4.6 3 K lượt thi 24 câu hỏi
🔥 Đề thi HOT:
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
Dạng 4: Trung điểm của đoạn thẳng có đáp án
Dạng 4: Một số bài tập nâng cao về lũy thừa
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
Dạng 1: Thực hiện tính, viết dưới dạng lũy thừa
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 2
Đề thi cuối học kỳ 2 Toán 6 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
Nội dung liên quan:
Danh sách câu hỏi:
Câu 8:
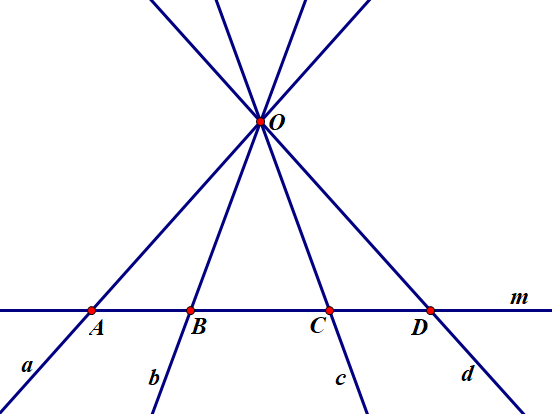
Giải thích vì sao hai đường thẳng phân biệt hoặc chỉ có một điểm chung hoặc không có điểm chung nào?
600 Đánh giá
50%
40%
0%
0%
0%