Giải SBT Toán 8 CTST Bài 1. Định lí Pythagore có đáp án

a) Áp dụng định lý Pythagore vào tam giác MNP vuông tại M, ta có:

NP² = MN² + MP² = 7² + 24² = 49 + 576 = 625.

Suy ra $NP=\sqrt{625}=25.$

b) Từ NP² = MN² + MP², suy ra MP² = NP² ‒ MN² = 29² ‒ 20² = 441.

Suy ra $MP=\sqrt{441}=21.$

c) Từ NP² = MN² + MP², suy ra MN² = NP² ‒ MP² = 61² ‒ 11² = 3600.

Suy ra $MN=\sqrt{3600}=60.$

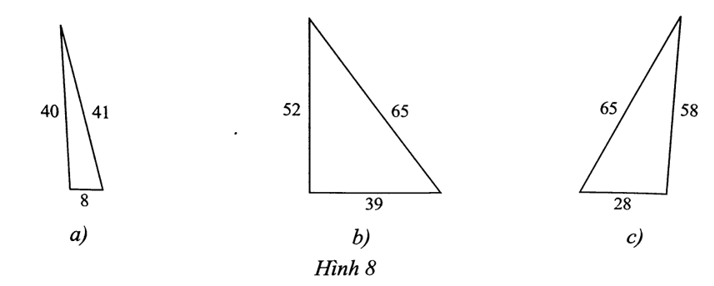
a) Ta có EG² = 37² = 1 369 và EF² + FG² = 35² + 12² = 1 369.

Suy ra tam giác EFG vuông tại F (định lí Pythagore đảo).

b) Ta có FG² = 85² = 7 225 và EF² + EG² = 77² + 36² = 7 225.

Suy ra tam giác EFG vuông tại E (định lí Pythagore đảo).

c) Ta có EF² = 13² = 169 và EG² + FG² = 12² + 5² = 169.

Suy ra tam giác EFG vuông tại G (định lí Pythagore đảo).

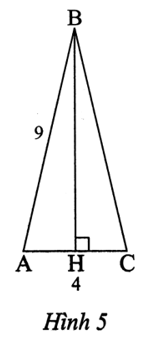
Tam giác ABC cân tại B nên đường cao BH cũng là đường trung tuyến.

Suy ra $\text{AH}=\frac{\text{AC}}{2}=\frac{4}{2}=2\left(cm\right)$

Áp dụng định lí Pythagore vào tam giác ABH vuông tại H, ta có:

AB² = AH² + BH²

Suy ra BH² = AB² – AH² = 9² – 2² = 77.

Do đó $\text{BH}=\sqrt{77}$ (cm).

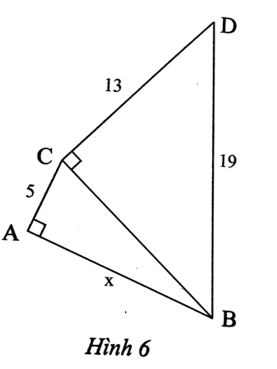
Áp dụng định lí Pythagore vào tam giác BCD vuông tại C, ta có:

BD² = BC² + CD²

Suy ra: BC² = BD² ‒ CD² = 19² ‒ 13² = 192.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:

BC² = AB² + AC²

Suy ra: AB² = BC² ‒ AC² = 192 ‒ 5² = 167.

Do đó $AB=x=\sqrt{167}$ (cm).

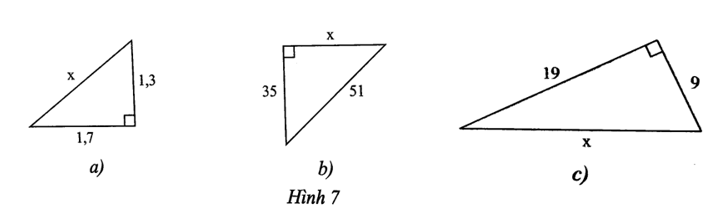
Áp dụng định lý Pythagore trong tam giác vuông ta có:

a) x² = 1,3² + 1,7² = 4,58

Suy ra: $x=\sqrt{\mathrm{4,58}}\approx \mathrm{2,1.}$

b) 51² = 35² + x²

Suy ra x² = 51² – 35² = 1376.

Do đó $\text{x}=\sqrt{1376}\approx 37.$

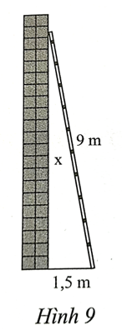
c) x² = 19² + 9² = 442.

Suy ra $x=\sqrt{442}\approx 21.$