Giải SGK Toán 12 CTST Bài 3. Sử dụng phần mềm GeoGebra để biểu diễn hình học tọa độ trong không gian có đáp án
38 người thi tuần này 4.6 385 lượt thi 4 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 1
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 9
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 8
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 7
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 6
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 5
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 3
Danh sách câu hỏi:
Lời giải
1. Khởi động phần mềm GeoGebra đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online. Chọn chế độ Vẽ đồ họa 3D với giao diện là một mặt phẳng nền để biểu diễn điểm, vectơ.
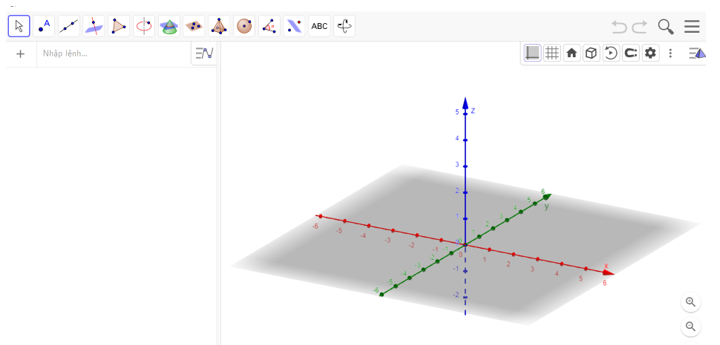
2. Các bước thao thác trên GeoGebra:
- Nhập tọa độ điểm: M(−2; −4; −5), N(3; 5; 0), P(0; 0; −2) vào vùng nhập lệnh theo cú pháp M(−2,−4,−5), N(3,5,0), P(0,0,−2).
- Nhập vectơ \(\overrightarrow v = \left( { - 2; - 4; - 5} \right)\), \(\overrightarrow a = \overrightarrow {MN} ,\) \(\overrightarrow b = \overrightarrow {NP} \) theo cú pháp v(−2,−4,−5); a=Vecto(M, N); b=Vecto(N, P).
3. Quan sát điểm, vectơ được vẽ trên vùng làm việc như hình bên dưới.
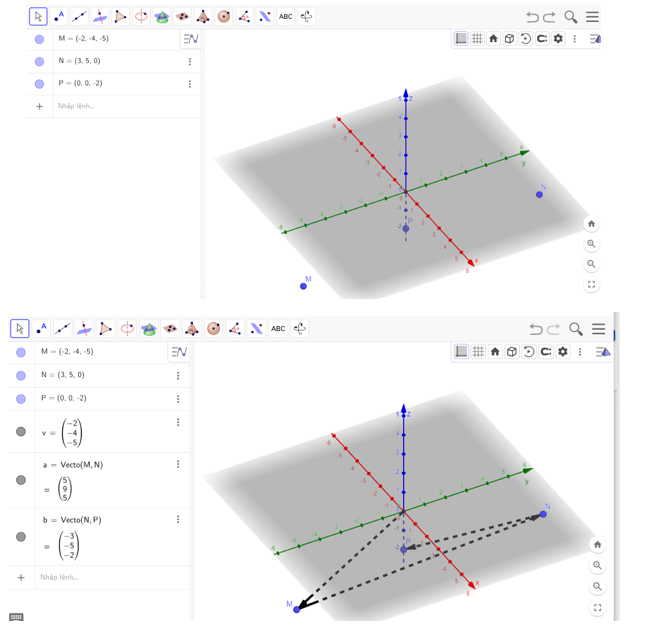
Lời giải
Mặt phẳng (P): 4x + 2y = 0
1. Khởi động phần mềm GeoGebra đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online. Chọn chế độ Vẽ đồ họa 3D với giao diện là một mặt phẳng nền để biểu diễn mặt phẳng.
2. Các bước thao thác trên GeoGebra:
Nhập mặt phẳng vào vùng nhập lệnh theo cú pháp: 4x + 2y = 0.
3. Quan sát mặt phẳng trên vùng làm việc
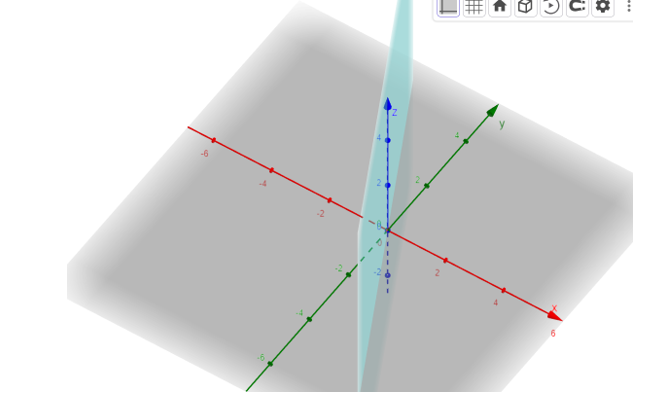
4. Sử dụng chuột để xoay hệ trục để có cảm nhận 3D trong không gian Oxyz.
Mặt phẳng (Q): x + y + z = 3
1. Khởi động phần mềm GeoGebra đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online. Chọn chế độ Vẽ đồ họa 3D với giao diện là một mặt phẳng nền để biểu diễn mặt phẳng.
2. Các bước thao thác trên GeoGebra:
Nhập mặt phẳng vào vùng nhập lệnh theo cú pháp: x + y + z = 3.
3. Quan sát mặt phẳng trên vùng làm việc
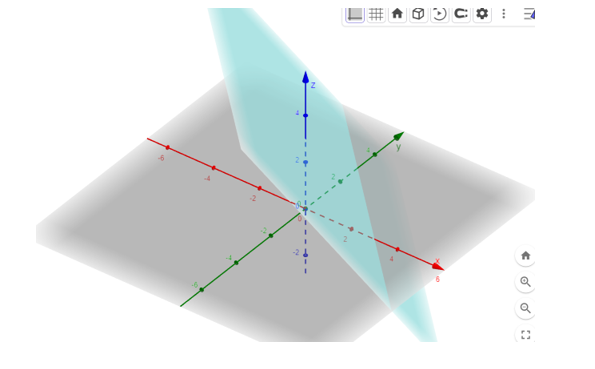
4. Sử dụng chuột để xoay hệ trục để có cảm nhận 3D trong không gian Oxyz.
Mặt phẳng (Q): z = 4
1. Khởi động phần mềm GeoGebra đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online. Chọn chế độ Vẽ đồ họa 3D với giao diện là một mặt phẳng nền để biểu diễn mặt phẳng.
2. Các bước thao thác trên GeoGebra:
Nhập mặt phẳng vào vùng nhập lệnh theo cú pháp: z = 4.
3. Quan sát mặt phẳng trên vùng làm việc
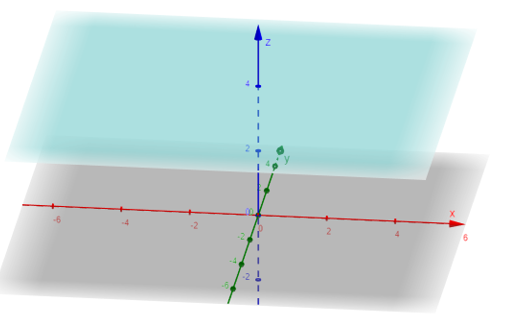
4. Sử dụng chuột để xoay hệ trục để có cảm nhận 3D trong không gian Oxyz.
Lời giải
1. Khởi động phần mềm GeoGebra đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online. Chọn chế độ Vẽ đồ họa 3D với giao diện là một mặt phẳng nền để biểu diễn đường thẳng.
2. Các bước thao thác trên GeoGebra:
Nhập phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 2 + 3t\\y = 5 - t\\z = - 3 + 4t\end{array} \right.\) vào vùng nhập lệnh theo cú pháp A(2,5,−3); u(3,−1,4); DuongThang(A,u).
3. Quan sát mặt phẳng trên vùng làm việc
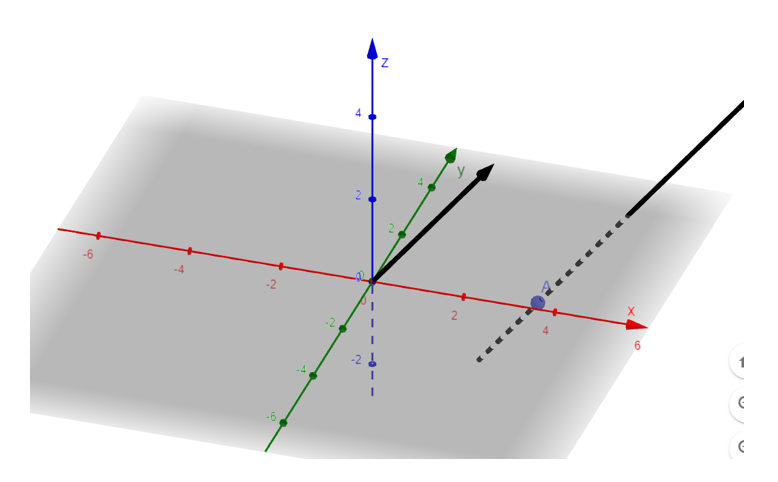
4. Sử dụng chuột để xoay hệ trục để có cảm nhận 3D trong không gian Oxyz.
Lời giải
Mặt cầu (S): x2 + y2 + z2 = 25
1. Khởi động phần mềm GeoGebra đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online. Chọn chế độ Vẽ đồ họa 3D với giao diện là một mặt phẳng nền để biểu diễn mặt cầu.
2. Các bước thao thác trên GeoGebra:
Nhập phương trình mặt cầu (S): x2 + y2 + z2 = 25 vào vùng nhập lệnh theo cú pháp I(0,0,0); R=5; MatCau(I,R).
3. Quan sát mặt phẳng trên vùng làm việc
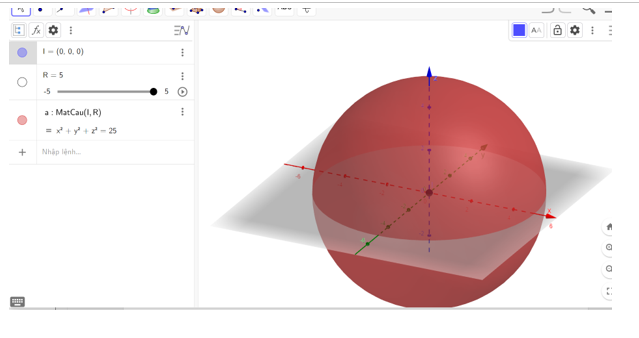
4. Sử dụng chuột để xoay hệ trục để có cảm nhận 3D trong không gian Oxyz.
Mặt cầu (S'): (x – 2)2 + (y + 3)2 + (z + 2)2 = 9.
1. Khởi động phần mềm GeoGebra đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online. Chọn chế độ Vẽ đồ họa 3D với giao diện là một mặt phẳng nền để biểu diễn mặt cầu.
2. Các bước thao thác trên GeoGebra:
Nhập phương trình mặt cầu (S'): (x – 2)2 + (y + 3)2 + (z + 2)2 = 9 vào vùng nhập lệnh theo cú pháp I(2,−3,−2); R=3; MatCau(I,R).
3. Quan sát mặt phẳng trên vùng làm việc
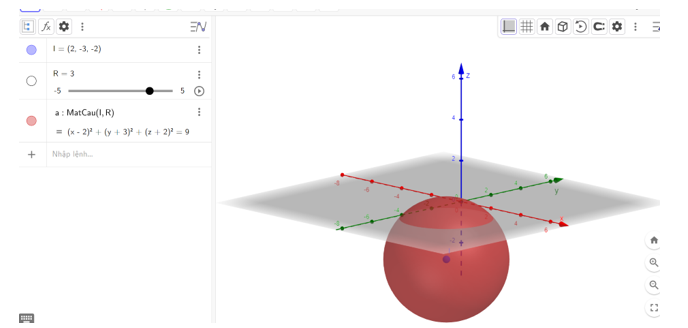
4. Sử dụng chuột để xoay hệ trục để có cảm nhận 3D trong không gian Oxyz.