Giải SBT Toán 12 Tập 1 KNTT Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đáp án

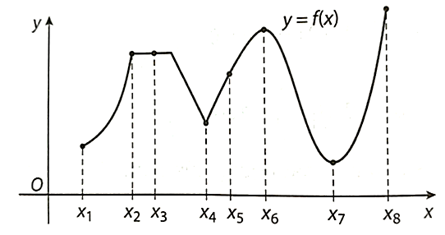
Quan sát đồ thị, ta thấy:

Hàm số đạt giá trị lớn nhất tại điểm x₈.

Hàm số đạt giá trị nhỏ nhất tại điểm x₇.

Hàm số đạt cực đại tại điểm x₆.

Hàm số đạt cực tiểu tại điểm x₄ và x₇.

a) y = 3x⁴ – 4x³

Tập xác định: D = ℝ.

Ta có: y' = 12x³ – 12x²

           y' = 0 ⇔ 12x³ – 12x² = 0 ⇔ x = 0 hoặc x = 1.

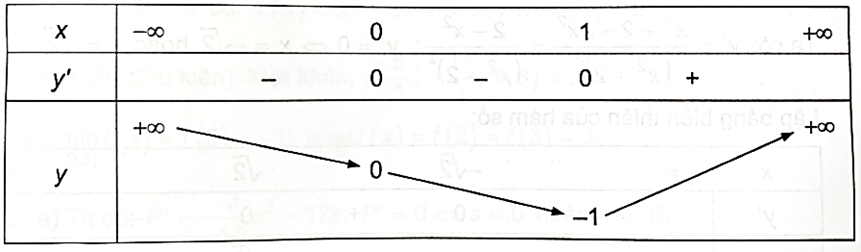
Từ bảng biến thiên, ta được \(\mathop {\min }\limits_\mathbb{R} y = y\left( 1 \right) = - 1\).

Hàn số không có giá trị lớn nhất.

b) \(y = \frac{{{x^2}}}{{x - 1}}\), x > 1

Tập xác định: D = (1; +∞).

Ta có: y' = \(\frac{{2x\left( {x - 1} \right) - {x^2}}}{{{{\left( {x - 1} \right)}^2}}}\) = \(\frac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}}\)

           y' = 0 ⇔ \(\frac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}}\) = 0 ⇔ x = 2 hoặc x = 0.

Do x > 1 nên x = 0 loại.

Ta có bảng biến thiên như sau:

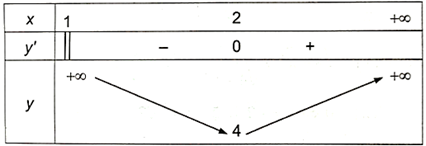
Từ bảng biến thiên, ta được: \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = y\left( 2 \right) = 4\).

Hàm số không có giá trị lớn nhất trên khoảng (1; +∞).

a) y = −x³ + 3x² + 2

Tập xác định: D = ℝ.

Ta có: y' = −3x² + 6x

           y' = 0 ⇔ −3x² + 6x = 0 ⇔ x = 0 hoặc x = 2.

Ta có bảng biến thiên như sau:

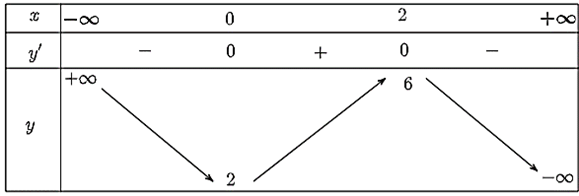
Từ bảng biến thiên, ta thấy hàm số không có cả giá trị lớn nhất và giá trị nhỏ nhất.

b) \(y = \frac{x}{{{x^2} + 2}}\)

Tập xác định: D = ℝ.

Ta có: y' = \(\frac{{{x^2} + 2 - 2{x^2}}}{{{{\left( {{x^2} + 2} \right)}^2}}}\) = \(\frac{{2 - {x^2}}}{{{{\left( {{x^2} + 2} \right)}^2}}}\)

           y' = 0 ⇔ \(\frac{{2 - {x^2}}}{{{{\left( {{x^2} + 2} \right)}^2}}}\) = 0 ⇔ x = ±\(\sqrt 2 \).

Ta có bảng biến thiên như sau:

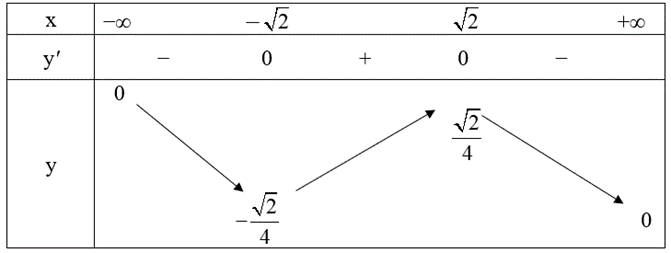
Từ bảng biến thiên, ta được:

\(\mathop {\min }\limits_\mathbb{R} y = y\left( { - \sqrt 2 } \right) = - \frac{{\sqrt 2 }}{4}\); \(\mathop {\max }\limits_\mathbb{R} y = y\left( {\sqrt 2 } \right) = \frac{{\sqrt 2 }}{4}\).

a) \(f(x) = x\sqrt {4 - {x^2}} \), −2 ≤ x ≤ 2

Ta có: f'(x) = \(\sqrt {4 - {x^2}} + \frac{{ - {x^2}}}{{\sqrt {4 - {x^2}} }}\) = \(\frac{{4 - 2{x^2}}}{{\sqrt {4 - {x^2}} }}\);

           f'(x) = 0 ⇔ x = ±\(\sqrt 2 \).

Ta tính được các giá trị: f(−2) = f(2) = 0; f(−\(\sqrt 2 \)) = −2; f(\(\sqrt 2 \)) = 2.

Do đó, \(\mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = f\left( { - \sqrt 2 } \right) = - 2\); \(\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = f\left( {\sqrt 2 } \right) = 2\).

b) f(x) = x – cosx, \( - \frac{\pi }{2} \le x \le \frac{\pi }{2}\)

Ta có: f'(x) = 1 + sinx

           f'(x) = 0 ⇔ 1 + sinx = 0 ⇔ x = \( - \frac{\pi }{2} + k2\pi \) (k ∈ ℤ).

Do \( - \frac{\pi }{2} \le x \le \frac{\pi }{2}\) nên x = \( - \frac{\pi }{2}\) (với k = 0).

Ta tính được các giá trị: \(f\left( {\frac{\pi }{2}} \right) = \frac{\pi }{2}\); \(f\left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}\).

Vậy \(\mathop {\min }\limits_{\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]} f\left( x \right) = f\left( { - \frac{\pi }{2}} \right) = - \frac{\pi }{2}\), \(\mathop {\max }\limits_{\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]} f\left( x \right) = f\left( {\frac{\pi }{2}} \right) = \frac{\pi }{2}\).

Xét x ∈ (0; 2), ta có: f(x) = 2x – 1

                                  f'(x) = 2 > 0 với mọi x ∈ (0; 2).

Mặt khác, ta có: f(0) = −1, f(2) = 3.

Xét x ∈ (2; 3), ta có: f(x) = x2 – 5x + 9

                                  f'(x) = 2x – 5

                                  f'(x) = 0 ⇔ x = \(\frac{5}{2}\) (thỏa mãn).

Mặt khác, f\(\left( {\frac{5}{2}} \right)\) = \(\frac{{11}}{4}\); f(3) = 3.