10 Bài tập Trường hợp đồng dạng thứ ba của tam giác (có lời giải)
37 người thi tuần này 4.6 343 lượt thi 10 câu hỏi 45 phút
🔥 Đề thi HOT:
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
9.2 K lượt thi
10 câu hỏi
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
15.3 K lượt thi
15 câu hỏi
20 câu trắc nghiệm Toán 8 Kết nối tri thức Ôn tập chương I (Đúng sai - trả lời ngắn) có đáp án
1.7 K lượt thi
20 câu hỏi
Trắc nghiệm Bài tập cơ bản Những hằng đẳng thức đáng nhớ có đáp án
2.9 K lượt thi
20 câu hỏi
3 câu Trắc nghiệm Toán 8 Bài 12: Hình vuông có đáp án (Vận dụng)
3.2 K lượt thi
3 câu hỏi
6 câu Trắc nghiệm Toán 8 Bài 11: Hình thoi có đáp án (Vận dụng)
3.2 K lượt thi
6 câu hỏi
10 câu Trắc nghiệm Toán 8 Bài 4: Phương trình tích có đáp án (Vận dụng)
3.2 K lượt thi
10 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
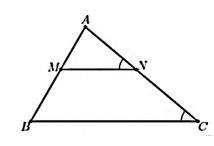
Câu 1
A. ΔANC ᔕ ΔMCN;
B. ΔANC ᔕ ΔAMC;
C. ΔABM ᔕ ΔANC;
D. ΔABM ᔕ ΔAMC.
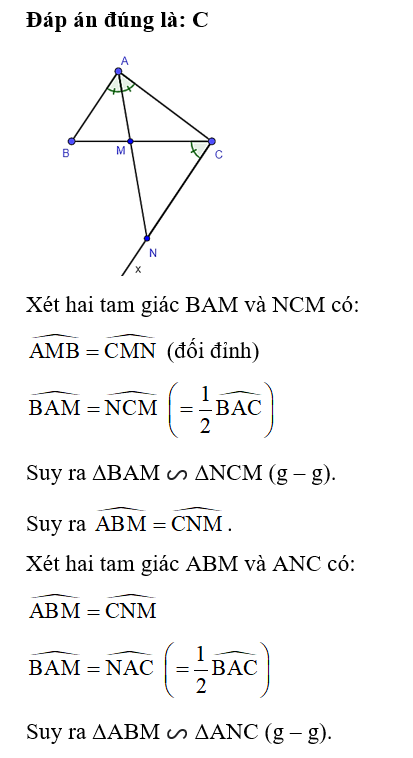
Lời giải
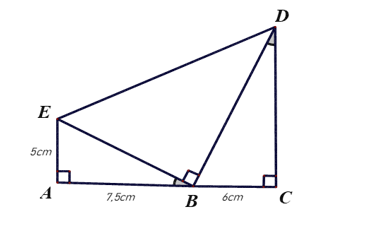
Câu 2
A. ΔABF ᔕ ΔEGD;
B. ΔGCF ᔕ ΔGDA;
C. ΔGCF ᔕ ΔABF
D. ΔABF ᔕ ΔGDA;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
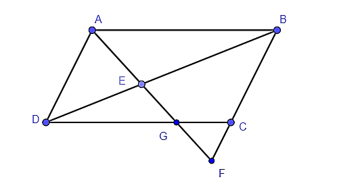
Xét hai tam giác GCF và GDA có:
(đối đỉnh)
(AD // BF, hai góc so le trong)
Suy ra ΔGCF ᔕ ΔGDA (g – g) (1).
Xét hai tam giác GCF và ABF có:
: Góc chung
(GC // BA, hai góc đồng vị)
Suy ra ΔGCF ᔕ ΔABF (g – g) (2).
Từ (1) và (2) suy ra ΔGDA ᔕ ΔABF.
Vậy A sai.
Câu 3
A. AB;
B. HC2;
C. AC2;
D. AB2.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
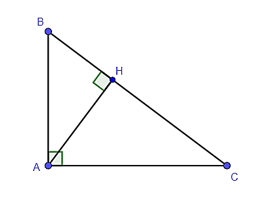
Xét hai tam giác BHA và BAC có:
: Góc chung
Suy ra ΔBHA ᔕ ΔBAC (g – g).
Suy ra .
Suy ra AB2 = BH ⋅ BC.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C
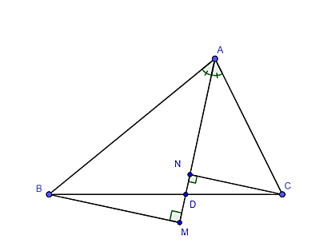
Xét hai tam giác ABM và ACN có:
(do AD là phân giác của góc A)
Suy ra ΔABM ᔕ ΔACN (g – g).
Suy ra .
Câu 5
A. AD ⋅ AB + AE ⋅ AF = AC2;
B. AB ⋅ AF + AE ⋅ AD = AC2;
C. AD ⋅ AF + AE ⋅ AB = AC2;
D. AD ⋅ AF ⋅ AE ⋅ AB = AC2.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C
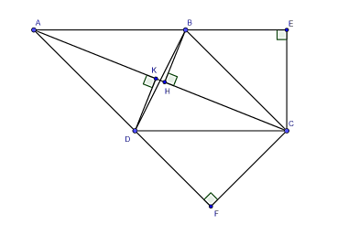
Xét tam giác AKD vuông tại K và tam giác CHB vuông tại H có:
AD = BC (do ABCD là hình bình hành)
(AD // BC, hai góc so le trong)
Do đó, ∆AKD = ∆CHB (cạnh huyền – góc nhọn).
Suy ra AK = HC.
Xét hai tam giác AHB và AEC có:
: Góc chung
Do đó, ΔAHB ᔕ ΔAEC (g – g).
Suy ra .
Suy ra AB ⋅ AE = AC ⋅ AH (1).
Xét hai tam giác ADK và ACF có
: Góc chung
Do đó, ΔADK ᔕ ΔACF (g – g).
Suy ra .
Suy ra AD ⋅ AF = AC ⋅ AK (2).
Lấy (1) + (2) ta được AB ⋅ AE + AD ⋅ AF = AC ⋅ AH + AC ⋅ AK
Lại có AC ⋅ AH + AC ⋅ AK = AC ⋅ (AH + AK) = AC ⋅ (AH + HC) = AC ⋅ AC = AC2.
Vậy AB ⋅ AE + AD ⋅ AF = AC2.
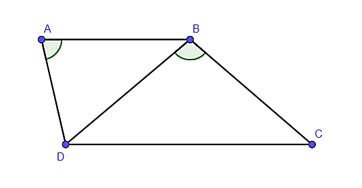
Câu 6
A. Tam giác MDC;
B. Tam giác DNC;
C. Tam giác ACM;
D. Tam giác NKB.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. ΔAMN ᔕ ΔABC;
B. AM ⋅ AN = AC ⋅ AB;
C. MN // BC;
D. AM ⋅ AC = AN ⋅ AB.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 14,6 cm;
B. 14,7 cm;
C. 14,69 cm;
D. 14 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
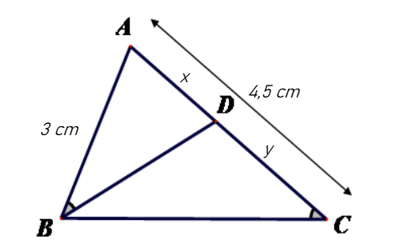
Câu 10
A. x = 3 cm, y = 1,5 cm;
B. x = 1,5 cm, y = 3 cm;
C. x = 2,5 cm, y = 2 cm;
D. x = 2 cm, y = 2,5 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập